2023-2024学年山东省德州市中职学校高三（上）第一次月考数学试卷

一、单项选择题。（本大题20个小题，每小题3分，共60分。在每小题列出的四个选项中，只有一项符合题目要求，请将符合题目要求的选项字母代号选出，并填涂在答题卡上）

• 1．已知集合A={a²，a}，则实数a满足的条件是（　　）

  A．a=0或a=1

  B．a=1

  C．a=0

  D．a≠0且a≠1
  组卷：26引用：1难度：0.8

  解析

• 2．满足条件{a,b}⊆B⊆{a,b,c,d,e}的所有集合B的个数是（　　）

  A．12

  B．6

  C．8

  D．16
  组卷：23引用：2难度：0.8

  解析

• 3．设集合A={4，5，7，9}，B={3，4，7，8，9}，全集U=A∪B，则集合∁_U（A∩B）中元素的个数为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：12引用：2难度：0.8

  解析

• 4．已知集合A={（x,y）|x+y=3}，B={（x,y）|x-2y=-3}，则A∩B=（　　）

  A．{（-1，2）}

  B．{1，2}

  C．{（1，2）}

  D．{-1，2}
  组卷：14引用：2难度：0.8

  解析

• 5．已知p：-2＜x＜-1，q：x²＞1，则p是q的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：33引用：1难度：0.7

  解析

• 6．若a,b均为实数，且a＞b,则下列关系正确的是（　　）

  A．-a＜-b

  B．a2＞b2

  C． a ＞ b

  D．|a|＞|b|
  组卷：18引用：1难度：0.9

  解析

• 7．设m=2a²+3a-6，n=3a²-a-2，其中a∈R，则（　　）

  A．m＞n

  B．m≥n

  C．m＜n

  D．m≤n
  组卷：20引用：1难度：0.8

  解析

• 8．设a,b∈R，且a＜b,则下列各式成立的是（　　）

  A．a2＜b2

  B．ac＜bc

  C． 1 a ＜ 1 b

  D．a-b＜0
  组卷：8引用：3难度：0.8

  解析

• 9．不等式-1≤-2x+3＜5的整数解有（　　）

  A．3个

  B．4个

  C．2个

  D．1个
  组卷：37引用：1难度：0.9

  解析

• 10．不等式|2-5x|≤0的解集为（　　）

  A．Φ

  B．R

  C． | x | x ≠ 2 5 ]

  D．{ 2 5 }
  组卷：35引用：1难度：0.8

  解析

三、解答题。（本大题5小题，共40分）

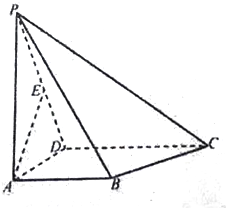• 29．如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA=AD，E为PD中点，AB∥CD且AB=

  1

  2

  CD

  ，AB⊥AD，求证：
  （1）AE⊥平面PCD；
  （2）AE∥平面PBC．
  ​
  组卷：58引用：1难度：0.7

  解析

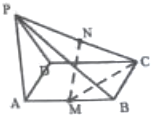• 30．如图所示，四棱锥P-ABCD的底面是边长为2的菱形，其中∠BAD=60°，PD⊥平面ABCD，点N是棱PC的中点，

  PD

  =

  2

  ．
  （1）求证：平面ANC⊥平面PDB；
  （2）求三棱锥N-ABC的体积．
  组卷：16引用：1难度：0.6

  解析