2023-2024学年湖北省十堰市郧西县八年级（上）期中数学试卷
发布：2024/9/27 15:0:1
一、选择题（每小题3分，共30分）
-
1．若三角形两边长分别是4、6，则第三边的长可能是（ ）
组卷：83引用：7难度：0.6 -
2．下列图案不是轴对称图形的是（ ）
组卷：48引用：5难度：0.9 -
3．下列图形中具有稳定性的是（ ）
组卷：56引用：5难度：0.7 -
4．一个多边形的每个外角都是40°，则这个多边形的内角和（ ）
组卷：219引用：10难度：0.8 -
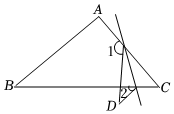5．如图，在△ABC中，∠C=43°，将△ABC沿着直线l折叠，点C落在点D的位置，则∠1-∠2的度数是（ ）组卷：49引用：1难度：0.7 -
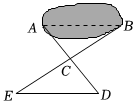6．如图，有一池塘，要测池塘两端A，B的距离，可先在地上取一个点C，从点C不经过池塘可以直接到达点A和B．连接AC并延长到点D，使CD=CA．连接BC并延长到点E，使CE=CB．连接DE，根据两个三角形全等，那么量出DE的长就知道A、B的距离．判断图中两个三角形全等的依据是（ ）组卷：39引用：1难度：0.7 -
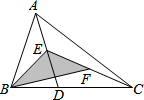7．如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=8cm2，则S阴影等于（ ）组卷：575引用：10难度：0.7 -
8．如图，△ABC的外角∠ACE和外角∠CAF的平分线交于点P，已知∠P=72°，则∠B的度数为（ ）组卷：84引用：4难度：0.6
三、解答题：（共72分）
-
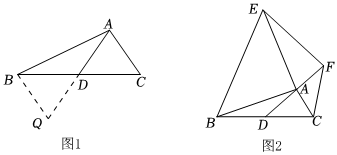23．阅读理解：课外兴趣小组活动时，老师提出了如下问题：在△ABC中，AB=7，AC=3，求BC边上的中线AD的取值范围．
（1）小明在组内经过合作交流，得到了如下的解决方法（如图1）：
①延长AD到Q使得DQ=AD；
②再连接BQ，把AB、AC、2AD集中在△ABQ中；③利用三角形的三边关系可得4＜AQ＜10，则AD的取值范围是 ．
感悟：解题时，条件中若出现“中点”“中线”等条件，可以考虑倍长中线，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中．
（2）请写出图1中AC与BQ的位置关系并证明；
（3）思考：已知，如图2，AD是△ABC的中线，AB=AE，AC=AF，∠BAE=∠FAC=90°，试探究线段AD与EF的数量和位置关系，并加以证明．组卷：887引用：17难度：0.4 -
24．如图，在平面直角坐标系中，点C（3，0），点A在y轴正半轴上，点B在x轴负半轴上，AB=AC，点D是x轴上的一动点（点D不与B、C重合），∠CAB=∠EAD=90°，AD=AE，连接CE．
（1）如图1，直接写出点A，B的坐标；
（2）如图2，当点D在边BC上时，求证：①BC=CE+CD，②BC⊥CE；
（3）当CD=5时，求点E的坐标．
组卷：371引用：4难度：0.4
