2022-2023学年浙江省台州市路桥区七年级（下）期末数学试卷

一、选择题（本题有10小题，每小题3分，共30分.请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分)

• 1．在平面直角坐标系中，下列各点位于第二象限的是（　　）

  A．（2，3）

  B．（2，-3）

  C．（-2，3）

  D．（-2，-3）
  组卷：205引用：5难度：0.8

  解析

• 2．为完成下列任务，采用抽样调查较合适的是（　　）

  A．对乘坐飞机的乘客进行安全检查

  B．了解七年级（1）班全体学生的身高

  C．了解小明同学某周每天参加体育运动的时间

  D．调查一批灯泡的使用寿命
  组卷：254引用：2难度：0.9

  解析

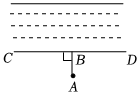• 3．如图，要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是（　　）

  A．两点之间线段最短	B．点到直线的距离
  C．两点确定一条直线	D．垂线段最短
  组卷：4672引用：41难度：0.9

  解析

• 4．估算

  13

  -1的值在（　　）

  A．1和2之间

  B．2和3之间

  C．3和4之间

  D．4和5之间
  组卷：1060引用：20难度：0.8

  解析

• 5．一元一次不等式组

  x - 3 ≥ 0

  x ＜ 4

  的解集为（　　）

  A．x＜4

  B．x≥3

  C．3≤x＜4

  D．无解
  组卷：76引用：3难度：0.7

  解析

• 6．如图，将直角三角形ABC沿AB方向平移得到直角三角形DEF．已知AD=4，AE=13，则DB长为（　　）

  A．4

  B．5

  C．9

  D．13
  组卷：1082引用：5难度：0.5

  解析

• 7．已知a＞b,则下列不等式不成立的是（　　）

  A．a+2＞b+2

  B．a-3＞b-3

  C．-4a＞-4b

  D． a 5 ＞ b 5
  组卷：229引用：4难度：0.7

  解析

• 8．如图是路政工程车的工作示意图，工作篮底部AB与支撑平台CD平行．若∠1=30°，∠3=150°，则∠2的度数为（　　）

  A．60°

  B．50°

  C．40°

  D．30°
  组卷：1194引用：12难度：0.6

  解析

三、解答题（本题有8小题，第17～19题每题6分，第20，21题每题8分，第22，23题每题10分，第24题12分，共66分）

• 23．在平面直角坐标系中，对于点P（x,y），若点Q的坐标为（ax+y,x+ay），则称点Q是点P的“a阶智慧点”（a为常数，且a≠0）．例如：点P（1，4）的“2阶智慧点”为点Q（2×1+4，1+2×4），即点Q（6，9）．
  （1）点A（-1，-2）的“3阶智慧点”的坐标为

  ．
  （2）若点B（2，-3）的“a阶智慧点”在第三象限，求a的整数解．
  （3）若点C（m+2，1-3m）的“-5阶智慧点”到x轴的距离为1，求m的值．
  组卷：1346引用：4难度：0.6

  解析

• 24．如图，有一张长方形纸条ABCD，AD∥BC，将四边形ABFE沿直线EF折叠，在线段DE，CF上分别取点G，H，连接GH，将四边形CDGH沿直线GH折叠，点A，B，C，D的对应点为点A′，B′，C′，D′，设∠EFB=α（0＜α＜90°）．
  （1）若C′D′在直线AD的上方，当α=50°且满足C′H∥B′F时，求∠CHG的度数．
  （2）在（1）的条件下，猜想直线EF和GH的位置关系，并证明．
  （3）在点G，H运动的过程中，若C′H∥B′F，请直接用含α的式子表示∠CHG的度数．
  
  组卷：367引用：2难度：0.3

  解析