2022-2023学年浙江省杭州市滨江区闻涛中学九年级(上)期中数学试卷
发布:2024/9/3 4:0:8
一、选择题。本大题有10个小题,每小题3分,共30分。
-
1.抛物线y=(x-1)2+5顶点坐标是( )
组卷:60引用:4难度:0.6 -
2.已知⊙O的半径是6cm,点P到圆心O的距离为4cm,则点P与⊙O的位置关系是( )
组卷:140引用:5难度:0.7 -
3.抛物线y=4x2与y=-4x2在同一平面直角坐标系内,下列说法不正确的是( )
组卷:48引用:3难度:0.6 -
 4.如图,点C是线段AB的黄金分割点(AC<BC),AB=8,则BC的长度是( )组卷:208引用:3难度:0.5
4.如图,点C是线段AB的黄金分割点(AC<BC),AB=8,则BC的长度是( )组卷:208引用:3难度:0.5 -
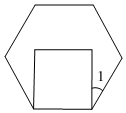 5.如图,在同一平面内,将边长相等的正六边形、正方形的一边重合,则∠1的度数为( )组卷:423引用:4难度:0.6
5.如图,在同一平面内,将边长相等的正六边形、正方形的一边重合,则∠1的度数为( )组卷:423引用:4难度:0.6 -
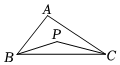 6.如图,点P是△ABC的重心,若△ABC的面积为12,则△BPC的面积为( )组卷:151引用:4难度:0.7
6.如图,点P是△ABC的重心,若△ABC的面积为12,则△BPC的面积为( )组卷:151引用:4难度:0.7 -
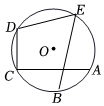 7.如图,点A,B,C,D,E在⊙O上,所对的圆心角为50°,则∠C+∠E等于( )ˆAB组卷:792引用:8难度:0.7
7.如图,点A,B,C,D,E在⊙O上,所对的圆心角为50°,则∠C+∠E等于( )ˆAB组卷:792引用:8难度:0.7
三、解答题。本大题有7个小题,共66分。解答应写出文字说明、证明过程或演算步骤。
-
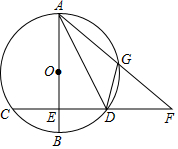 22.已知:如图,AB是圆O的直径,CD是圆O的弦,AB⊥CD,E为垂足,AE=CD=8,F是CD延长线上一点,连接AF交圆O于G,连接AD、DG.
22.已知:如图,AB是圆O的直径,CD是圆O的弦,AB⊥CD,E为垂足,AE=CD=8,F是CD延长线上一点,连接AF交圆O于G,连接AD、DG.
(1)求圆O的半径;
(2)求证:△ADG∽△AFD;
(3)当点G是弧AD的中点时,求△ADG的面积与△AFD的面积比.组卷:1395引用:6难度:0.1 -
23.如图,在Rt△ABC中,∠CAB=90°,AC=3,AB=4,AD⊥BC于点D,射线CE平行AB交AD的延长线于点E,P是射线CE上一点(在点E的右侧),连结AP交BC于点F.
(1)求证:△ACE∽△BAC.
(2)若,求CEEP=35的值.PFAF
(3)以PF为直径的圆经过△BDE中的某一个顶点时,求所有满足条件的EP的长.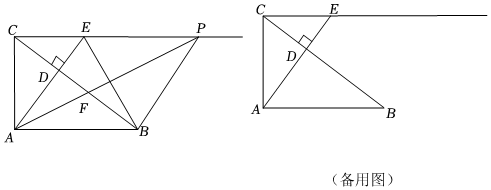 组卷:799引用:6难度:0.2
组卷:799引用:6难度:0.2


