2021-2022学年山西省阳泉市盂县七年级（上）期末数学试卷
发布：2024/7/10 8:0:8
一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请将正确的答案填在答题卡上相应的表格内）
-
1．围成下列这些立体图形的各个面中，都是平的面为（ ）
组卷：140引用：2难度：0.7 -
2．下表是2021年12月21日我国几个城市的最低气温，在这些城市中，最低气温最低的城市是（ ）
城市 北京 上海 沈阳 海南 太原 新疆 最低气温 -3℃ 7℃ -13℃ 15℃ -10℃ -6℃ 组卷：30引用：1难度：0.9 -
3．多项式2x2-x+1的各项分别是（ ）
组卷：17引用：1难度：0.7 -
4．中国人对方程的研究有悠久的历史．中国古代数学著作《九章算术》中有专门以“方程”命名的一章．中国古代数学家表示方程时，只用算筹表示各未知数的系数，而没有使用专门的记法来表示未知数．1859年中国清代一位数学家在翻译外国数学著作时，开始将equation（指含有未知数的等式）一词译为“方程”，至今一直这样沿用．这位清代数学家是（ ）
组卷：41引用：1难度：0.8 -
5．根据下面所给条件，能列出方程的是（ ）
组卷：67引用：3难度：0.9 -
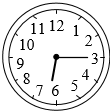6．小明晚上放学到家时，钟表的时间显示为6点15分（如图），此时时钟的分针与时针所成角的度数是（ ）组卷：105引用：2难度：0.7 -
7．若a、b表示非零常数，整式ax+b的值随x的取值而发生变化．如下表：
则关于x的一元一次方程-ax-b=-3的解是（ ）x -3 -1 0 1 3 … ax+b -3 1 3 5 9 … 组卷：66引用：2难度：0.6
三、解答题（本大题共8个小题，共75分．解答应写出文字说明、证明过程或演算步骤）
-
22．操作与实践：在综合与实践活动课上，老师将一副三角板按图1所示的位置摆放，分别在∠AOC，∠BOD的内部作射线OM，ON，然后提出如下问题：先添加一个适当条件，再求∠MON的度数．
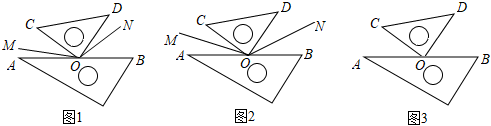
（1）特例探究：“兴趣小组”的同学添加了：“若OM，ON分别平分∠AOC，∠BOD”，画出如图2所示图形．小组3号同学佳佳的做法：由于图中∠AOC与∠BOD的和为90°，所以我们容易得到∠MOC与∠NOD的和，这样就能求出∠MON的度数．请你根据佳佳的做法，写出解答过程．
（2）特例探究：“发现小组”的同学添加了：“若∠MOC=∠AOC，∠DON=13∠BOD”，画出如图3所示图形．小组2号同学乐乐的做法：设∠AOC的度数为x°，我们就能用含有x°的式子表示出∠COM和∠DON的度数，这样就能求出∠MON的度数，请你根据乐乐的做法，写出解答过程．13
（3）类比拓展：受“兴趣小组”和“发现小组”的启发，“创新小组”的同学添加了：“若∠MOC=∠AOC，∠DON=1n∠BOD”．请你直接写出∠MON的度数．1n组卷：134引用：2难度：0.5 -
23．综合探究
【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：如图①，若数轴上点A、点B表示的数分别为a,b（b＞a），则线段AB的长（点A到点B的距离）可表示为b-a.请用上面材料中的知识解答下面的问题：
【问题情境】如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达点A，再向右移动3个单位长度到达点B，然后再向右移动5个单位长度到达点C．
（1）【问题探究】请在图②中表示出A、B、C三点的位置；
（2）【问题探究】若点P从点A出发，以每秒1个单位长度的速度沿数轴向左匀速运动，同时点M、N从点B、点C分别以每秒2个单位长度、每秒3个单位长度速度沿数轴向右匀速运动．设移动时间为t秒（t＞0）．
①A，B两点间的距离AB=，AC=；
②若点D、E分别是线段AB，BC的中点，求线段DE的长；
③用含t的代数式表示：t秒时，点P表示的数为 ，点M表示的数为 ，点N表示的数为 ；
④试探究在移动的过程中，3PN-4PM的值是否随着时间t的变化而变化？若变化说明理由；若不变，请求其值．组卷：1480引用：6难度：0.4
