2022-2023学年江苏省淮安市清河区开明中学八年级（下）期末数学试卷

一、选择题（本大题共8小题，每小题3分，共24分）

• 1．围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史．下列由黑白棋子摆成的图案是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：96引用：2难度：0.9

  解析

• 2．下列调查方式中适合的是（　　）

  A．要了解一批节能灯的使用寿命，采用普查方式

  B．调查全市中学生每天的就寝时间，采用普查方式

  C．要调查你所在班级同学的视力情况，采用抽样调查方式

  D．环保部门调查京杭大运河某段水域的水质情况，采用抽样调查方式
  组卷：217引用：5难度：0.9

  解析

• 3．要反映经开区2023年5月份每天的最高气温的变化情况，宜采用（　　）

  A．统计表

  B．扇形统计图

  C．条形统计图

  D．折线统计图
  组卷：33引用：2难度：0.7

  解析

• 4．下列分式中，属于最简分式的是（　　）

  A． a - 1 a 2 - 1

  B． 2 x - 1

  C． 6 3 x

  D． 1 - m m - 1
  组卷：364引用：6难度：0.6

  解析

• 5．下列事件中，不可能事件是（　　）

  A．掷一枚质地均匀的正方体骰子，掷得的点数不是奇数就是偶数

  B．从一副扑克牌中任意抽出一张，其花色是黑桃

  C．从装满红球的袋子中摸出白球

  D．抛一枚普通的硬币，出现正面朝上
  组卷：31引用：2难度：0.7

  解析

• 6．当x满足什么条件时，分式

  x

  -

  2

  x

  +

  2

  的值为0．（　　）

  A．x=-2

  B．x=2

  C．x≠-2

  D．x≠2
  组卷：201引用：2难度：0.7

  解析

• 7．已知a,b是两个连续整数，a＜

  3

  -1＜b,则a,b分别是（　　）

  A．-2，-1

  B．-1，0

  C．0，1

  D．1，2
  组卷：1467引用：15难度：0.7

  解析

• 8．若点A（x₁，-6），B（x₂，-2），C（x₃，2）在反比例函数y=

  12

  x

  的图象上，则x₁，x₂，x₃的大小关系是（　　）

  A．x1＜x2＜x3

  B．x2＜x1＜x3

  C．x2＜x3＜x1

  D．x3＜x2＜x1
  组卷：2733引用：20难度：0.7

  解析

三、解答题（本大题共9小题，共72分，请在答题卡指定区域内作答，解答应写出必要的文字说明、证明过程或演算步骤）

• 24．定义：有一组对边平行，有一个内角是它对角的两倍的凸四边形叫做倍角梯形．
  
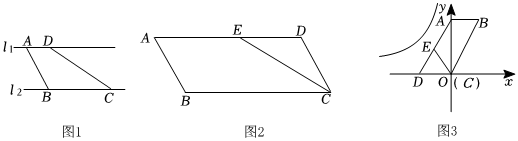
  如图1，直线l₁∥l₂，点A、D在直线l₁上，点B、C在直线l₂上，若∠BAD=2∠BCD，则四边形ABCD是倍角梯形．
  （1）如图2，点E是▱ABCD的边AD上一点，∠A=60°，AB=2，AE=3．若四边形ABCE是倍角梯形，则BC的长是

  ；
  （2）如图3，以▱ABCD的顶点C为坐标原点，边CD所在直线为x轴，对角线AC所在直线为y轴，建立平面直角坐标系．点E是边AD上一点，满足BC=AE+CE．求证：四边形ABCE是倍角梯形；
  （3）在（2）的条件下，当AB=AE=2，∠B=60°时，将四边形ABCE向左平移a（a＞0）个单位后，恰有两个顶点落在反比例函数y=

  k

  x

  的图象上，直接写出k的值．
  组卷：267引用：2难度：0.1

  解析

• 25．【性质探究】
  
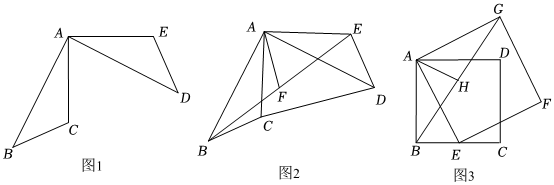
  （1）如图1，将△ABC绕点A逆时针旋转90°得到△ADE，
  ①则DE与BC的位置关系为

  ；
  ②如图2，连接CD、BE，若点F为BE的中点，连接AF，请探究线段AF与CD的关系，并说明理由；
  【拓展应用】
  （2）如图3，已知点E是正方形ABCD的边BC上任意一点，以AE为边作正方形AEFG，连接BG，点H为BG的中点，连接AH．若AB=2，BE=1，则AH的长为

  ．
  组卷：247引用：1难度：0.4

  解析