当前位置：试卷中心 > 试卷详情

2023-2024学年北京九十六中九年级（上）期中数学试卷

发布：2024/9/29 9:0:1

一、选择题（每题2分，共16分）第1-8题均有四个选项，符合题意的选项只有一个。

1．古典园林中的窗户是中国传统建筑装饰的重要组成部分，一窗一姿容，一窗一景致．下列窗户图案中，是中心对称图形的是（　　）
A． B． C． D．
组卷：292引用：22难度：0.9
解析
2．二次函数y=2（x-3）²+1的图象的顶点坐标是（　　）
A．（2，3） B．（2，1） C．（3，-1） D．（3，1）
组卷：965引用：16难度：0.8
解析
3．二次函数y=x²+2的图象向左平移1个单位长度，得到的二次函数解析式为（　　）
A．y=x²+3 B．y=（x-1）²+2 C．y=x²+1 D．y=（x+1）²+2
组卷：219引用：5难度：0.6
解析
4．已知⊙O的半径是5，OP的长为7，则点P与⊙O的位置关系是（　　）
A．点P在圆内 B．点P在圆上 C．点P在圆外 D．不能确定
组卷：69引用：6难度：0.7
解析
5．下列事件中是随机事件的是（　　）
A．明天太阳从东方升起
B．经过有交通信号灯的路口时遇到红灯
C．平面内不共线的三点确定一个圆
D．任意画一个三角形，其内角和是540°
组卷：494引用：17难度：0.8
解析
6．如图，点A，B，C在⊙O上，△OAB是等边三角形，则∠ACB的大小为（　　）
A．60° B．30° C．40° D．20°
组卷：769引用：9难度：0.7
解析
7．如图，⊙O是正方形ABCD的外接圆，若⊙O的半径为4，则正方形ABCD的边长为（　　）
A．4 B．8 C．
2
2
D．
4
2
组卷：1063引用：9难度：0.5
解析
8．如图，正方形ABCD和⊙O的周长之和为20cm,设圆的半径为x cm,正方形的边长为y cm,阴影部分的面积为S cm²．当x在一定范围内变化时，y和S都随x的变化而变化，则y与x,S与x满足的函数关系分别是（　　）
A．一次函数关系，一次函数关系
B．一次函数关系，二次函数关系
C．二次函数关系，二次函数关系
D．二次函数关系，一次函数关系
组卷：1586引用：11难度：0.7
解析

二、填空题（共16分，每题2分）

9．请写出一个开口向下，且与y轴的交点坐标为（0，2）的抛物线的表达式：
．
组卷：541引用：14难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共68分）解答应写出文字说明、演算步骤或证明过程。

27．如图1，在△ABC中，∠ACB=90°，CA=CB，点D，E分别在边CA，CB上，CD=CE，连接DE，AE，BD．点F在线段BD上，连接CF交AE于点H．
（1）①比较∠CAE与∠CBD的大小，并证明；
②若CF⊥AE，求证：AE=2CF；
（2）将图1中的△CDE绕点C逆时针旋转α（0°＜α＜90°），如图2．若F是BD的中点，判断AE=2CF是否仍然成立．如果成立，请证明；如果不成立，请说明理由．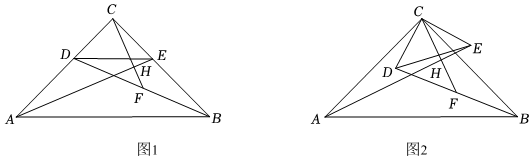
组卷：1351引用：4难度：0.3
解析
28．在平面直角坐标系xOy中，⊙O的半径为1，点A在⊙O上，点P在⊙O内，给出如下定义：连接AP并延长交⊙O于点B，若AP=kAB，则称点P是点A关于⊙O的k倍特征点．
（1）如图，点A的坐标为（1，0）．
①若点P的坐标为（-
1
2
，0），则点P是点A关于⊙O的
倍特征点；
②在C₁（0，
1
2
），C₂（
1
2
，0），C₃（
1
2
，-
1
2
）这三个点中，点
是点A关于⊙O的
1
2
倍特征点；
③直线l经过点A，与y轴交于点D，∠DAO=60°．点E在直线l上，且点E是点A关于⊙O的
1
2
倍特征点，求点E的坐标；
（2）若当k取某个值时，对于函数y=-x+1（0＜x＜1）的图象上任意一点M，在⊙O上都存在点N，使得点M是点N关于⊙O的k倍特征点，直接写出k的最大值和最小值．
组卷：685引用：8难度：0.2
解析