2021年江苏省扬州市广陵区树人学校中考数学三轮复习试卷（1）

一、选择题（共5小题，每小题3分，满分15分）

• 1．下列各组数中，把两数相乘，积为1的是（　　）

  A．2和-2

  B．-2和 1 2

  C． 3 和 3 3

  D． 3 和- 3
  组卷：1181引用：13难度：0.9

  解析

• 2．在平面直角坐标系中，将点P（0，1）绕坐标原点O顺时针旋转90°，所得到的对应点P′的坐标为（　　）

  A．（1，0）

  B．（-1，0）

  C．（0，-1）

  D．（1，1）
  组卷：267引用：3难度：0.6

  解析

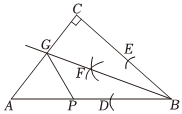• 3．如图，Rt△ABC中，∠C=90°，利用尺规在BC，BA上分别截取BE，BD，使BE=BD；分别以D，E为圆心、以大于

  1

  2

  DE的长为半径作弧，两弧在∠CBA内交于点F；作射线BF交AC于点G．若△BCG的面积为4，BC=4，P为AB上一动点，则GP的最小值为（　　）

  A．无法确定

  B．4

  C．3

  D．2
  组卷：193引用：7难度：0.7

  解析

• 4．如图，在Rt△ABC中，∠C=90°，AC=2cm,AB=4cm,点P从点C出发，以2cm/s的速度沿折线CA→AB→BC运动，最终回到C点，设点P的运动时间为x,线段CP的长度为y,则能反映y与x之间的函数关系的图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：164引用：3难度：0.6

  解析

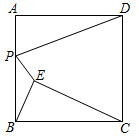• 5．如图，已知正方形ABCD的边长为8，点E是正方形内部一点，连接BE，CE，且∠ABE=∠BCE，点P是AB边上一动点，连接PD，PE，则PD+PE长度的最小值为（　　）

  A．8 2

  B．4 10

  C．8 5 -4

  D．4 13 -4
  组卷：1494引用：6难度：0.4

  解析

三、解答题

• 14．在平面直角坐标系xOy中，已知抛物线y=ax²-2ax+a-2（a＞0）．分别过点M（t,0）和点N（t+2，0）作x轴的垂线，交抛物线于点A和点B．记抛物线在A，B之间的部分为图象G（包括A，B两点）．
  （1）求抛物线的顶点坐标；
  （2）记图象G上任意一点的纵坐标的最大值与最小值的差为m.
  ①当a=2时，若图象G为轴对称图形，求m的值；
  ②若存在实数t,使得m=2，直接写出a的取值范围．
  组卷：2207引用：5难度：0.1

  解析

• 15．在平面直角坐标系xOy中，对于点A和线段MN，如果点A，O，M，N按逆时针方向排列构成菱形AOMN，且∠AOM=α，则称线段MN是点A的“α-相关线段”．例如，图1中线段MN是点A的“30°-相关线段”．
  （1）已知点A的坐标是（0，2）．
  ①在图2中画出点A的“30°-相关线段”MN，并直接写出点M和点N的坐标；
  ②若点A的“α-相关线段”经过点（

  3

  ，1），求α的值；
  （2）若存在α，β（α≠β）使得点P的“α-相关线段”和“β-相关线段”都经过点（0，4），记PO=t,直接写出t的取值范围．
  
  组卷：1227引用：7难度：0.1

  解析