2023-2024学年贵州省遵义市绥阳县部分学校八年级（上）期中数学试卷
发布：2024/9/27 19:0:1
一、选择题（每小题3分，共36分）
-
1．若一个三角形的两边长分别是3和4，则第三边的长可能是（ ）
组卷：150引用：6难度：0.9 -
2．如图图形中，不是轴对称图形的是（ ）
组卷：27引用：3难度：0.9 -
3．一个多边形的内角和是1260°，这个多边形的边数是（ ）
组卷：783引用：28难度：0.7 -
4．如图，△ABE≌△ACF．若AB=5，AE=2，BE=4，则CF的长度是（ ）组卷：189引用：9难度：0.7 -
5．如图，王师傅用4根木条钉成一个四边形木架，要使这个木架不变形，他至少要再钉上木条的根数是（ ）组卷：1513引用：29难度：0.9 -
6．如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带（ ）去．组卷：4403引用：150难度：0.9 -
7．等腰三角形的一个角是80°，则它顶角的度数是（ ）
组卷：2118引用：197难度：0.9 -
8．如图，将含30°角的三角板的直角顶点放在直尺的一边上，若∠1=40°，则∠2的度数为（ ）组卷：100引用：5难度：0.7
三、解答题
-
24．如图，已知∠MAN=120°，AC平分∠MAN．B、D分别在射线AN、AM上．
（1）在图（1）中，当∠ABC=∠ADC=90°时，求证：AD+AB=AC．
（2）若把（1）中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°，其他条件不变，如图（2）所示．则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．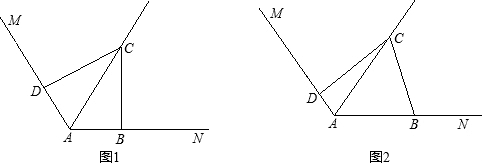
组卷：711引用：16难度：0.5 -
25．（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m,CE⊥直线m,垂足分别为点D、E．证明：DE=BD+CE．
（2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
（3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．
组卷：11394引用：145难度：0.5
