当前位置：试卷中心 > 试卷详情

2022-2023学年安徽省芜湖市无为市八年级（下）期中数学试卷

发布：2024/6/10 8:0:9

1．若式子
x
+
2
在实数范围内有意义，则x的取值范围是（　　）
A．x＞-2 B．x＜-2 C．x≠-2 D．x≥-2
组卷：686引用：45难度：0.9
解析
2．下列二次根式，不能与
2
合并的是（　　）
A．
1
2
B．
8
C．
12
D．-
18
组卷：557引用：15难度：0.9
解析
3．点O为矩形ABCD对角线AC与BD的交点，若AC=6，则OD的长为（　　）
A．1 B．2 C．3 D．6
组卷：254引用：6难度：0.9
解析
4．下列式子中，为最简二次根式的是（　　）
A．
14
B．
8
C．
1
5
D．
1
.
2
组卷：144引用：4难度：0.7
解析
5．在直角三角形中，两直角边的长分别为6和12，则斜边上中线的长为（　　）
A．3
3
B．3
5
C．6
3
D．6
5
组卷：29引用：4难度：0.7
解析
6．在△ABC中，∠A，∠B，∠C的对边分别记为a,b,c,下列条件中，能判定△ABC是直角三角形的是（　　）
A．a²=（c-b）（c+b） B．a=1，b=2，c=3
C．∠A=∠C D．∠A：∠B：∠C=3：4：5
组卷：728引用：10难度：0.5
解析
7．将一个有45°角的三角尺的直角顶点C放在一张宽为3cm的纸带边沿上，另一个顶点A在纸带的另一边沿上，测得三角尺的一边AC与纸带的一边所在的直线成30°角，如图，则三角尺的最长边的长为（　　）
A．6 B．3
2
C．4
2
D．6
2
组卷：628引用：6难度：0.7
解析

22．如图，在平行四边形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，AE=CG，AH=CF，且EG平分∠HEF．
（1）求证：△AEH≌△CGF．
（2）若∠EFG=90°．求证：四边形EFGH是正方形．
组卷：1995引用：14难度：0.7
解析
23．综合与实践
【问题情境】
数学活动课上，老师出示了一个问题：如图1，在正方形ABCD中，E是BC的中点，AE⊥EP，EP与正方形的外角∠DCG的平分线交于P点．试猜想AE与EP的数量关系，并加以证明；
【思考尝试】
（1）同学们发现，取AB的中点F，连接EF可以解决这个问题．请在图1中补全图形，解答老师提出的问题．
【实践探究】
（2）希望小组受此问题启发，逆向思考这个题目，并提出新的问题：如图2，在正方形ABCD中，E为BC边上一动点（点E，B不重合），△AEP是等腰直角三角形，∠AEP=90°，连接CP，可以求出∠DCP的大小，请你思考并解答这个问题．
【拓展迁移】
（3）突击小组深入研究希望小组提出的这个问题，发现并提出新的探究点：如图3，在正方形ABCD中，E为BC边上一动点（点E，B不重合），△AEP是等腰直角三角形，∠AEP=90°，连接DP．知道正方形的边长时，可以求出△ADP周长的最小值．当AB=4时，请你求出△ADP周长的最小值．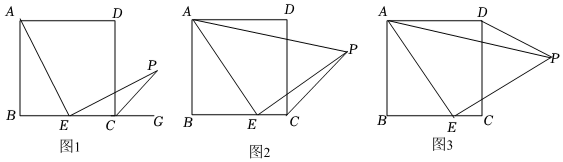
组卷：3230引用：19难度：0.3
解析

A．a²=（c-b）（c+b）	B．a=1，b=2，c=3
C．∠A=∠C	D．∠A：∠B：∠C=3：4：5

1．若式子x+2在实数范围内有意义，则x的取值范围是（ ）