2022-2023学年山西省运城市夏县九年级（上）期中数学试卷

一、选择题（本大题共10个小题，每小题3分，共30分.在每个小题给出的四个选项，只有一项符合题目要求）

• 1．一元二次方程x²-2x=0的根是（　　）

  A．x=2

  B．x=0

  C．x1=-2，x2=0

  D．x1=2，x2=0
  组卷：300引用：18难度：0.9

  解析

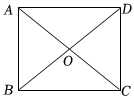• 2．如图，四边形ABCD是平行四边形，添加下列一个条件不能判定四边形ABCD为矩形的是（　　）
  ​

  A．AB⊥BC

  B．∠DAB=∠ABC

  C．AC=BD

  D．∠DAB=∠BCD
  组卷：12引用：1难度：0.5

  解析

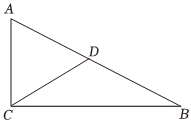• 3．如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，AC=5，BC=12，则CD的长为（　　）​

  A．13

  B．12

  C．6.5

  D．6
  组卷：6引用：1难度：0.6

  解析

• 4．如图，在小提琴的设计中，蕴含着数学知识，AC，BC，AB各部分长度的比满足

  AC

  BC

  =

  BC

  AB

  =

  5

  -

  1

  2

  ，这体现了数学中的（　　）
  ​

  A．黄金分割

  B．平移

  C．旋转

  D．轴对称
  组卷：232引用：5难度：0.8

  解析

• 5．用配方法解方程x²+4x-5=0，下列配方正确的是（　　）

  A．（x+2）2=1

  B．（x+2）2=5

  C．（x+2）2=9

  D．（x+4）2=9
  组卷：1247引用：22难度：0.9

  解析

• 6．已知关于x的方程x²-（2m+1）x+m²=0有两个不相等的实数根，则m的取值范围是（　　）

  A．m＞- 1 4

  B．m＞- 1 2

  C．m≥- 1 4

  D．m≥- 1 2
  组卷：52引用：2难度：0.5

  解析

• 7．为执行国家药品降价政策，给人民群众带来实惠，某药品经过两次降价，每盒零售价由25元降为16元，设平均每次降价的百分率是x,则根据题意，下列方程正确的是（　　）

  A．25（1-2x）2=16	B．25（1-x）2=16
  C．25（1-2x）=16	D．25（1-x）=16
  组卷：11引用：1难度：0.7

  解析

• 8．下列四个三角形中，与图中△ABC的相似的是（　　）

  A．

  B．

  C．

  D．
  组卷：344引用：6难度：0.7

  解析

三、解答题（本大题共8个小题，共75分。解答应写出文字说明、证明过程或演算步骤）

• 23．综合与实践
  【问题情境】
  如图1，点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．
  （1）求证：四边形CEGF是正方形．
  （2）求

  AG

  BE

  的值．
  【类比探究】
  （3）如图2，将正方形的CEGF绕点C按顺时针方向旋转α（0°＜α＜45°），试探究线段AG与BE长度之间的数量关系，并说明理由．
  组卷：413引用：2难度：0.3

  解析

• 24．如图，在四边形ABCD中，AB∥CD，∠ADC=90°，AC⊥BC．
  （1）求证：△ACB∽△CDA．
  （2）若DC=6cm,AD=8cm,点P从A点出发，以2cm/s的速度沿AB向终点B匀速运动，同时点Q从B点出发，以1cm/s的速度沿BC向终点C匀速运动．当其中一点到达终点时，两点都停止运动，设运动时间为t（s）
  ①t为何值时，四边形APQC的面积等于

  170

  3

  c

  m

  2

  ？
  ②是否存在某一时刻t,使得以B，P，Q为顶点的三角形与△ADC相似？若存在，请直接写出t的值；若不存在，请说明理由．
  组卷：48引用：3难度：0.4

  解析