2022-2023学年北京159中九年级（上）期中数学试卷

一、选择题（本题共16分，每小题2分，其中只有一个是符合题意的）

• 1．下列图形中，既是中心对称，又是轴对称的是（　　）

  A．

  B．

  C．

  D．
  组卷：66引用：4难度：0.9

  解析

• 2．二次函数y=（x-1）²+3图象的顶点坐标是（　　）

  A．（1，3）

  B．（1，-3）

  C．（-1，3）

  D．（-1，-3）
  组卷：2862引用：42难度：0.6

  解析

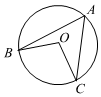• 3．如图，点A，B，C均在⊙O上，∠BOC=100°，则∠BAC的度数为（　　）

  A．70°

  B．60°

  C．50°

  D．40°
  组卷：1454引用：20难度：0.8

  解析

• 4．若将抛物线y=5x²先向右平移2个单位，再向上平移1个单位，得到的新抛物线的表达式为（　　）

  A．y=5（x-2）2+1	B．y=5（x+2）2+1
  C．y=5（x-2）2-1	D．y=5（x+2）2-1
  组卷：1486引用：43难度：0.7

  解析

• 5．方程x²-3x+1=0的根的情况是（　　）

  A．有两个相等实数根	B．有两个不相等实数根
  C．没有实数根	D．无法判断
  组卷：672引用：14难度：0.8

  解析

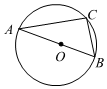• 6．如图，AB是⊙O的直径，点C是⊙O上一点，若∠BAC=30°，BC=2，则AB的长为（　　）

  A．2

  B．4

  C．6

  D．8
  组卷：516引用：6难度：0.8

  解析

• 7．某市严格落实国家节水政策，2018年用水总量为6.5亿立方米，2020年用水总量为5.265亿立方米．设该市用水总量的年平均降低率是x,那么x满足的方程是（　　）

  A．6.5（1-x）2=5.265	B．6.5（1+x）2=5.265
  C．5.265（1-x）2=6.5	D．5.265（1+x）2=6.5
  组卷：1574引用：24难度：0.6

  解析

• 8．已知：如图，直线

  y

  =

  4

  3

  x

  -

  4

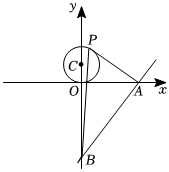  与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB．则△PAB面积的最大值是（　　）

  A．9

  B．20

  C．5

  D．10
  组卷：51引用：1难度：0.6

  解析

二、填空题（共8小题，每小题3分，满分24分）

• 9．若关于x的方程x²-kx-12=0的一个根为2，则k的值为

  ．
  组卷：220引用：7难度：0.8

  解析

三、解答题（本题共60分，第17题6分，第18，19题每题4分，第20题3分，第21-25题每题5分，第26题6分，第27-28题每题6分）

• 27．在等腰直角△ABC中，∠CAB=90°，F是射线AC上一动点（不与A、C重合），作射线BF，过点C作CG⊥BF于点G，连接AG．
  
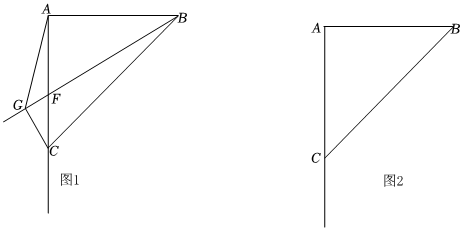
  （1）如图1，当点F在线段AC上时．①求证：∠ABG=∠ACG；②用等式表示AG，BG，CG之间的等量关系，并证明．
  （2）如图2，当点F在AC延长线上时，请直接用等式表示AG，BG，CG之间的等量关系．
  组卷：80引用：2难度：0.3

  解析

• 28．对于平面直角坐标系xOy中第一象限内的点P（x,y）和图形W，给出如下定义：过点P作x轴和y轴的垂线，垂足分别为M，N，若图形W中的任意一点Q（a,b）满足a≤x且b≤y,则称四边形PMON是图形W的一个覆盖，点P为这个覆盖的一个特征点．
  例：已知A（1，2），B（3，1），则点P（5，4）为线段AB的一个覆盖的特征点．
  （1）已知：A（1，2），B（3，1），点C（2，3），
  ①在P₁（1，3），P₂（3，3），P₃（4，4）中，是△ABC的覆盖特征点的为

  ；
  ②若在一次函数y=mx+6（m≠0）的图象上存在△ABC的覆盖的特征点，求m的取值范围．
  （2）以点D（3，4）为圆心，半径为1作圆，在抛物线y=ax²-5ax+4（a≠0）上存在⊙D的覆盖的特征点，直接写出a的取值范围

  ．
  
  组卷：249引用：4难度：0.3

  解析