2022-2023学年安徽省安庆四中九年级(上)期中数学试卷
发布:2024/8/26 6:0:10
一.选择题(本大题共10小题,每小题4分,满分40分)
-
1.下列函数中,是二次函数的为( )
组卷:845引用:14难度:0.9 -
2.如图所示,三个三角形中,相似的是( )
 组卷:136引用:2难度:0.5
组卷:136引用:2难度:0.5 -
3.在同一平面直角坐标系中,一次函数y=ax+b与二次函数y=b(x-a)2的图象大致为( )
组卷:356引用:8难度:0.6 -
4.已知:
(x,y,z均不为零),则x6=y4=z3=( )x+3y3y-2z组卷:535引用:6难度:0.9 -
5.若反比例函数y=
的图象经过点(3,1),则它的图象也一定经过的点是( )kx组卷:125引用:2难度:0.9 -
6.鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例,是自然界最美的鬼斧神工.如图,P是AB的黄金分割点(AP>BP),若线段AB的长为6cm,则AP的长约为( )
 组卷:280引用:2难度:0.6
组卷:280引用:2难度:0.6 -
7.将抛物线先向下平移2个单位长度,再向左平移1个单位长度后,所得抛物线的函数表达式为y=(x-3)2-4,则原抛物线的函数表达式为( )
组卷:21引用:2难度:0.5
七.解答题(本题12分)
-
22.某水果店销售一种新鲜水果,平均每天可售出120箱,每箱盈利60元,为了扩大销售减少库存,水果店决定采取适当的降价措施,经调查发现,每箱水果每降价5元,水果店平均每天可多售出20箱.设每箱水果降价x元.
(1)当x=10时,每箱利润 元,平均每天可售出 箱水果;
(2)设每天销售该水果的总利润为w元.
①求w与x之间的函数解析式;
②试判断w能否达到8200元,如果能达到,求出此时x的值;如果不能达到,求出w的最大值.组卷:159引用:4难度:0.4
八.解答题(本题14分)
-
23.[初步尝试]
(1)如图①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
[思考说理]
(2)如图②,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与点C重合,折痕为MN,求的值;AMBM
[拓展延伸]
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B′处,折痕为CM.
①求线段AC的长;
②若点O是边AC的中点,点P为线段OB′上的一个动点,将△APM沿PM折叠得到△A′PM,点A的对应点为点A′,A′M与CP交于点F,求的取值范围.PFMF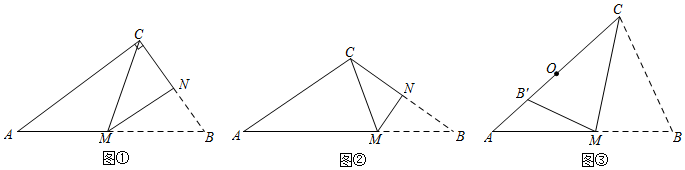 组卷:5197引用:17难度:0.1
组卷:5197引用:17难度:0.1


