2023-2024学年江苏省南通市启东市折桂中学九年级（上）月考数学试卷（10月份）

一、（本大题共10小题，每小题3分，共30分在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）

• 1．抛物线y=x²-2x+4的顶点坐标是（　　）

  A．（1，3）

  B．（1，-3）

  C．（-1，-3）

  D．（-1，3）
  组卷：1281引用：7难度：0.8

  解析

• 2．将抛物线y=x²-3向左平移2个单位后得到的抛物线表达式是（　　）

  A．y=x2-1

  B．y=x2-5

  C．y=（x+2）2-3

  D．y=（x-2）2-3
  组卷：1140引用：8难度：0.6

  解析

• 3．在平面直角坐标系中，抛物线y=x²-2mx+m²+2m+1的顶点一定不在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：2866引用：8难度：0.6

  解析

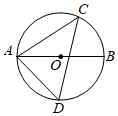• 4．如图，AB为⊙O的直径，点C、点D是⊙O上的两点，连接CA，CD，AD．若∠CAB=35°，则∠ADC的度数是（　　）

  A．40°

  B．45°

  C．55°

  D．100°
  组卷：683引用：6难度：0.6

  解析

• 5．筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图1．筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2．已知圆心O在水面上方，且⊙O被水面截得的弦AB长为6米，⊙O半径长为4米．若点C为运行轨道的最低点，则点C到弦AB所在直线的距离是（　　）
  

  A．1米

  B．（4- 7 ）米

  C．2米

  D．（4+ 7 ）米
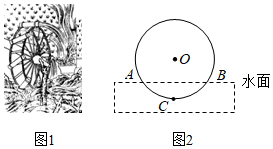  组卷：3214引用：41难度：0.7

  解析

• 6．若二次函数y=kx²-4x-2与x轴有两个不同的交点，则k的取值范围是（　　）

  A．k＞-2

  B．k＞-2且k≠0

  C．k＜2

  D．k≥-2且k≠0
  组卷：378引用：5难度：0.8

  解析

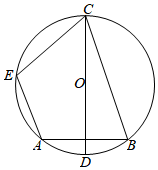• 7．如图，在⊙O中，点D为

  ˆ

  AB

  的中点，CD为⊙O的直径，AE∥BC交⊙O于点E．连接CE．若∠ECD=50°，则∠DCB=（　　）

  A．10°

  B．15°

  C．20°

  D．25°
  组卷：595引用：3难度：0.6

  解析

• 8．如图，抛物线y=-x²+mx的对称轴为直线x=2，若关于x的一元二次方程-x²+mx-t=0（t为实数）在1≤x≤3的范围内有解，则t的取值错误的是（　　）

  A．t=2.5

  B．t=3

  C．t=3.5

  D．t=4
  组卷：1625引用：13难度：0.5

  解析

三、解答题（本大题共8小题，共90分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

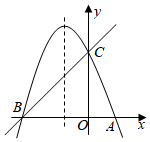• 25．如图，已知抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
  （1）求抛物线的解析式；
  （2）在抛物线的对称轴上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标及此时距离之和的最小值；
  （3）如果点P（x₁，n）和点Q（x₂，n）在函数y=ax²+bx+c的图象上，且x₁＜x₂，PQ=2m,求

  x

  2

  1

  -mx₂-3m+6的值．
  组卷：366引用：4难度：0.3

  解析

• 26．定义：平面直角坐标系xOy中，点P（a,b），点Q（c,d），若c=ka,d=-kb,其中k为常数，且k≠0，则称点Q是点P的“k级变换点”．例如，点（-4，6）是点（2，3）的“-2级变换点”．
  （1）函数y=-

  4

  x

  的图象上是否存在点（1，2）的“k级变换点”？若存在，求出k的值；若不存在，说明理由；
  （2）动点A（t,

  1

  2

  t-2）与其“k级变换点”B分别在直线l₁，l₂上，在l₁，l₂上分别取点（m²，y₁），（m²，y₂）．若k≤-2，求证：y₁-y₂≥2；
  （3）关于x的二次函数y=nx²-4nx-5n（x≥0）的图象上恰有两个点，这两个点的“1级变换点”都在直线y=-x+5上，求n的取值范围．
  组卷：4853引用：6难度：0.3

  解析