2020-2021学年山西省晋中市灵石县九年级(上)期中数学试卷
发布:2024/9/11 7:0:8
一、选择题(每小题3分,共30分)
-
 1.如图,直线a∥b∥c,若BC=10,AB=4,DE=6,则EF的长为( )组卷:181引用:6难度:0.5
1.如图,直线a∥b∥c,若BC=10,AB=4,DE=6,则EF的长为( )组卷:181引用:6难度:0.5 -
2.方程x2=3x的解为( )
组卷:2643引用:80难度:0.9 -
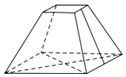 3.如图所示的几何体的左视图应为( )组卷:206引用:3难度:0.9
3.如图所示的几何体的左视图应为( )组卷:206引用:3难度:0.9 -
4.若
,则ba=25的值为( )a-ba+b组卷:1269引用:10难度:0.9 -
 5.如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为( )组卷:1713引用:30难度:0.9
5.如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为( )组卷:1713引用:30难度:0.9 -
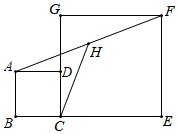 6.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=6,H是AF的中点,那么CH的长是( )组卷:1701引用:9难度:0.6
6.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=6,H是AF的中点,那么CH的长是( )组卷:1701引用:9难度:0.6 -
7.关于x的方程(m-1)x2-2x+1=0有两个不相等的实数根,则实数m的取值范围是( )
组卷:745引用:5难度:0.9
三、解答题(共75分)
-
22.综合与实践
【问题情境】在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.
如图1,将:矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD.并且量得AB=2cm,AC=4cm.
【操作发现】
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到如图2所示的△AC′D,过点C作AC′的平行线,与DC′的延长线交于点E,请你判断四边形ACEC′的形状,并证明你的结论.
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B、A、D三点在同一条直线上,得到如图3所示的△AC′D,连接CC′,取CC′的中点F,连接AF并延长至点G,使FG=AF,连接CG、C′G,得到四边形ACGC′,请你判断四边形ACGC′的形状,并证明你的结论.
【实践探究】
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A′点,A′C与BC′相交于点H,如图4所示,连接CC′,直接写出线段C′H的长度.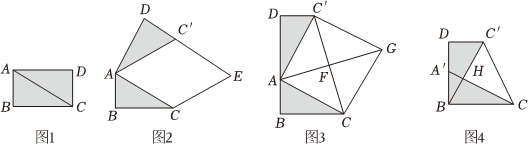 组卷:115引用:1难度:0.2
组卷:115引用:1难度:0.2 -
23.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点P从点A出发,沿线段AB以每秒5个单位长度的速度向终点B运动.当点P不与点A、B重合时,过点P作PQ⊥AB,交折线AC-CB于点Q,过点P、Q分别平行于BC、BA的直线相交于点R.设点P运动的时间为t秒.
(1)求出线段PQ的长.(用含t的代数式表示)
(2)当点R落在边AC上时,求t的值.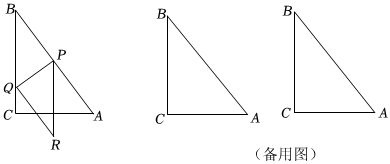 组卷:11引用:1难度:0.1
组卷:11引用:1难度:0.1


