2022-2023学年广东省广州113中九年级（上）期中数学试卷

一、选择题（本题有10个小题，每小题3分，满分30分。）

• 1．方程x²=4x的解是（　　）

  A．x=4

  B．x=2

  C．x=4或x=0

  D．x=0
  组卷：437引用：102难度：0.9

  解析

• 2．观察下列银行标志，从图案看既是轴对称图形又是中心对称图形的有（　　）个．
  

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：253引用：66难度：0.9

  解析

• 3．已知x₁，x₂是方程x²-2x-3=0的两根，则x₁x₂=（　　）

  A．-2

  B．2

  C．-3

  D．3
  组卷：44引用：6难度：0.9

  解析

• 4．若关于x的一元二次方程x²+x-3m=0有两个不相等的实数根，则m的取值范围是（　　）

  A．m＞ 1 12

  B．m＜ 1 12

  C．m＞ - 1 12

  D．m＜ - 1 12
  组卷：282引用：16难度：0.9

  解析

• 5．若抛物线

  y

  =

  （

  m

  +

  1

  ）

  x

  m

  2

  -

  2

  的开口向上，则m的值为（　　）

  A．2

  B．-2

  C．±2

  D．1
  组卷：457引用：6难度：0.5

  解析

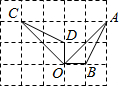• 6．如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O按逆时针方向旋转而得，则旋转的角度为（　　）

  A．30°

  B．45°

  C．90°

  D．135°
  组卷：1691引用：148难度：0.9

  解析

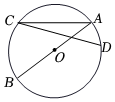• 7．如图，AB是⊙O的直径，∠ACD=15°，则∠BAD的度数为（　　）

  A．75°

  B．72°

  C．70°

  D．65°
  组卷：78引用：1难度：0.7

  解析

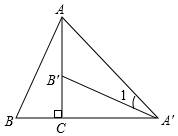• 8．如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，若∠B=60°，则∠1的度数是（　　）

  A．15°

  B．25°

  C．10°

  D．20°
  组卷：295引用：9难度：0.9

  解析

三、解答题（本题有9个小题，共72分，解答要求写出文字说明，证明过程或计算步骤。）

• 24．如图，△ABC是等边三角形，点D是BC边的中点，以D为顶点作一个120°的角，角的两边分别交直线AB、AC于M、N两点，以点D为中心旋转∠MDN（∠MDN的度数不变）．
  
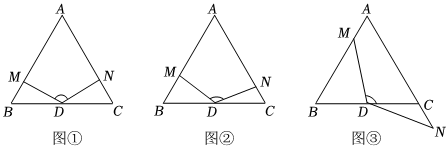
  （1）如图①，若DM⊥AB，求证：BM+CN=BD；
  （2）如图②，若DM与AB不垂直，且点M在边AB上，点N在边AC上时，（1）中的结论是否成立？并说明理由；
  （3）如图③，若DM与AB不垂直，且点M在边AB上，点N在边AC的延长线上时，（1）中的结论是否成立？若不成立，写出BM、CN、BD之间的数量关系，并说明理由．
  组卷：37引用：2难度：0.1

  解析

• 25．已知抛物线y=mx²+（1-2m）x+1-3m与x轴相交于不同的两点A、B
  （1）求m的取值范围；
  （2）证明该抛物线一定经过非坐标轴上的一点P，并求出点P的坐标；
  （3）当

  1

  4

  ＜m≤8时，由（2）求出的点P和点A，B构成的△ABP的面积是否有最值？若有，求出该最值及相对应的m值．
  组卷：4486引用：8难度：0.1

  解析