2022-2023学年湖南省衡阳市衡南一中九年级（上）联赛检测数学试卷

一、单选题（共8个小题，每小题5分，共40分）

• 1．已知xy＜0，化简二次根式

  -

  x

  y

  2

  y

  的值是（　　）

  A． x

  B． - x

  C． - x

  D． - - x
  组卷：715引用：3难度：0.6

  解析

• 2．根据下列表格的对应值：判断方程x²+x-1=0一个解的取值范围是（　　）
  

  x	0.59	0.60	0.61	0.62	0.63
  x2+x-1	-0.061	-0.04	-0.018	0.0044	0.027

  A．0.59＜x＜0.60	B．0.60＜x＜0.61
  C．0.61＜x＜0.62	D．0.62＜x＜0.63
  组卷：204引用：20难度：0.6

  解析

• 3．4件外观相同的产品中只有1件不合格，现从中一次抽取2件进行检测，抽到的两件产品中有一件产品合格而另一件产品不合格的概率是（　　）

  A． 3 8

  B． 1 3

  C． 2 3

  D． 1 2
  组卷：390引用：6难度：0.6

  解析

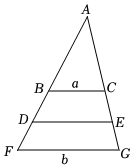• 4．如图，一定能够得到a∥b的条件有几个？（　　）
  （1）

  AD

  DF

  =

  AE

  EG

  ；
  （2）

  AB

  AF

  =

  BC

  FG

  ；
  （3）

  BD

  DF

  =

  CE

  EG

  ；
  （4）△ABC与△AFG相似．

  A．3个

  B．2个

  C．1个

  D．0个
  组卷：56引用：3难度：0.7

  解析

• 5．三角函数sin40°、cos16°、tan50°之间的大小关系是（　　）

  A．tan50°＞cos16°＞sin40°	B．cos16°＞sin40°＞tan50°
  C．cos16°＞tan50°＞sin40°	D．tan50°＞sin40°＞cos16
  组卷：587引用：4难度：0.7

  解析

• 6．关于x的一元二次方程x²-mx+2m-1=0的两个实数根分别是x₁、x₂，且x₁²+x₂²=7，则（x₁-x₂）²的值是（　　）

  A．1

  B．12

  C．13

  D．25
  组卷：1214引用：56难度：0.9

  解析

四、解答题（共60分）

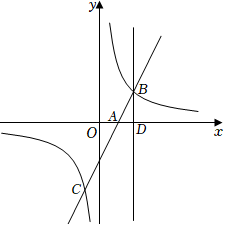• 18．已知一元二次方程ax²+bx+2=0（a≠0）有两个相等的实数根．
  （1）求a,b满足的关系式；
  （2）求b-a的最大值，并求此时a,b的值；
  （3）在（2）的条件下，直线y=2x-a与x轴交于点A，与双曲线y=

  b

  x

  相交于B，C两点（点B在点C的右侧），过点B作直线BD⊥x轴，垂足为点D，过点C的直线交x轴于点E，交直线BD于点F，若△EDF∽△BDA，求点E的坐标．
  组卷：160引用：2难度：0.5

  解析

• 19．（1）如图1，四边形ABCD是正方形，点E是AD边上的一个动点，以CE为边在CE的右侧作正方形CEFG，连接DG、BE，判断线段DG与BE的数量关系并说明理由；
  （2）如图2，四边形ABCD是矩形，AB=3，BC=6，点E是AD边上的一个动点，以CE为边在CE的右侧作矩形CEFG，且CG：CE=1：2，连接DG、BE．判断线段DG与BE又有怎样的数量关系，并说明理由；
  （3）如图3，在（2）的条件下，连接BG，求2BG+BE的最小值．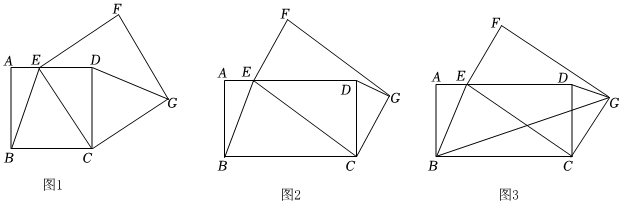
  
  组卷：520引用：5难度：0.3

  解析