2022-2023学年安徽省六安市金安区皋城中学九年级(上)期中数学试卷
发布:2024/9/6 2:0:8
一、选择题(每小题4分,共40分)
-
1.一次函数y=-2x+1的图象不经过( )
组卷:2731引用:97难度:0.9 -
2.抛物线y=2(x-3)2-7的顶点坐标是( )
组卷:212引用:6难度:0.6 -
3.若点A(-2,y1),B(-1,y2)都在反比例函数y=
的图象上,则y1,y2的大小关系是( )2x组卷:1243引用:7难度:0.6 -
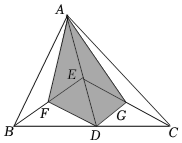 4.如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则四边形AFDG的面积是( )组卷:259引用:4难度:0.6
4.如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则四边形AFDG的面积是( )组卷:259引用:4难度:0.6 -
5.已知点C是线段AB的黄金分割点,AC>BC,若AB=2,则AC的长为( )
组卷:356引用:6难度:0.7 -
6.将抛物线y=
向右平移3个单位长度,再向上平移3个单位长度,则平移后所得到的抛物线解析式是( )14x2组卷:50引用:4难度:0.7 -
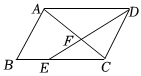 7.如图,在平行四边形ABCD中,E为边BC上一点,AC与DE相交于点F,若CE=2EB,△AFD面积为18,则△EFC的面积等于( )组卷:18引用:3难度:0.6
7.如图,在平行四边形ABCD中,E为边BC上一点,AC与DE相交于点F,若CE=2EB,△AFD面积为18,则△EFC的面积等于( )组卷:18引用:3难度:0.6
六、(每小题12分,共24分)
-
22.为了落实劳动教育,某学校邀请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量y千克与每平方米种植的株数x(2≤x≤8,且x为整数)构成一种函数关系.每平方米种植2株时,平均单株产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少0.5千克.
(1)求y关于x的函数表达式.
(2)每平方米种植多少株时,能获得最大的产量?最大产量为多少千克?组卷:2312引用:18难度:0.6
七、(本大题14分)
-
23.在矩形ABCD中,点O是对角线AC、BD的交点,直角∠EPF的顶点P与O重合,OE、OF分别与AB、BC边相交于E、F,连接EF,BC=k•AB(k为常数).
(1)发现问题:如图1,若k=1,猜想=.OEOF
(2)类比探究:如图2,k≠1,探究线段OE,OF之间的数量关系,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,若FO=FC,k=,OD=22,求EF的长.6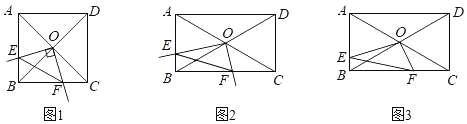 组卷:229引用:6难度:0.4
组卷:229引用:6难度:0.4


