2022-2023学年湖北省武汉市蔡甸区九年级(下)月考数学试卷(2月份)
发布:2024/7/24 8:0:9
一、选择题(共10小题,每小题3分,共30分)
-
1.将一元二次方程2x2+x=3化成一般形式之后,若二次项的系数是2,则一次项系数和常数项分别是( )
组卷:658引用:5难度:0.9 -
2.下列图案中,既是轴对称图形又是中心对称图形的是( )
组卷:968引用:11难度:0.8 -
3.盒子里有10个球,它们只有颜色不同,其中红球有7个,黄球有2个,黑球有1个.幸幸从中任意摸一个球,下面说法正确的是( )
组卷:303引用:4难度:0.8 -
4.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
组卷:1096引用:81难度:0.9 -
5.将一元二次方程x2-6x+7=0化成(x+a)2=b的形式,下列变形正确的是( )
组卷:83引用:3难度:0.5 -
6.抛物线y=-
x2向右平移1个单位长度得到新抛物线的解析式为( )12组卷:54引用:3难度:0.6 -
7.某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,则现年20岁的这种动物活到25岁的概率为( )
组卷:59引用:3难度:0.8 -
8.点A(m,y1),B(m+3,y2)都在y=(x-1)2+n上,若y2≥y1,则m的取值范围是( )
组卷:698引用:3难度:0.5
三、解答题(共8题,共72分)
-
23.(1)如图,点P为等腰直角△ABC内一点(∠ABC=90°,AB=BC),∠APB=135°判断线段PA、PB、PC之间的数量关系,并说明理由;
变式:
(2)如图,点P为等腰直角△ABC外一点(∠ABC=90°,AB=BC),∠APB=45°,判断线段PA、PB、PC之间的数量关系,并说明理由;
拓展:
(3)如图,PA=3,PB=4,以AB为边作等腰Rt△ABC,∠ABC=90°,直接写出PC的最大值.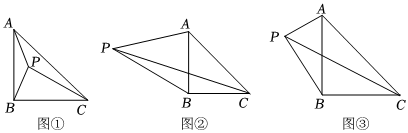 组卷:345引用:2难度:0.2
组卷:345引用:2难度:0.2 -
24.已知抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,交y轴于点C,M是抛物线顶点.
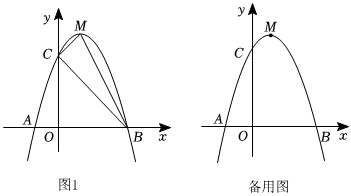
(1)直接写出抛物线的函数解析式;
(2)如图1,点P在抛物线上,若直线AP经过△CBM外接圆的圆心,判断△CBM的形状并求点P的横坐标;
(3)以点P(1,t)为圆心的⊙P与x轴相切且与抛物线只有两个公共点,求t的取值范围.组卷:360引用:2难度:0.2


