2022-2023学年四川大学附中九年级（上）入学数学试卷

一.选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）

• 1．下列图形中，不是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：263引用：12难度：0.9

  解析

• 2．下列因式分解正确的是（　　）

  A．ab+ac+a=a（b+c）	B．a2-4b2=（a+4b）（a-4b）
  C．9a2+6a+1=3a（3a+2）+1	D．a2-4ab+4b2=（a-2b）2
  组卷：298引用：4难度：0.8

  解析

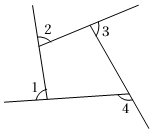• 3．如图，已知∠1+∠2+∠3=240°，那么∠4的度数为（　　）

  A．60°

  B．120°

  C．130°

  D．150°
  组卷：821引用：17难度：0.7

  解析

• 4．如图，在△ABC中，AB=AC=13，BC=10，AD⊥BC于点D，则AD的长为（　　）

  A．10

  B．11

  C．12

  D．13
  组卷：685引用：2难度：0.5

  解析

• 5．已知x=2是分式方程

  k

  x

  +

  x

  -

  1

  x

  -

  3

  =

  1

  的解，那么k的值为（　　）

  A．0

  B．1

  C．2

  D．4
  组卷：897引用：6难度：0.7

  解析

• 6．如图，l₁反映了某产品的销售收入与销售量之间的关系，l₂反映了该产品的销售成本与销售量之间的关系，当销售收入大于销售成本时，该产品才开始盈利．根据图中信息判断该公司在盈利时的销售量为（　　）

  A．小于4件

  B．大于4件

  C．等于4件

  D．不小于4件
  组卷：336引用：6难度：0.5

  解析

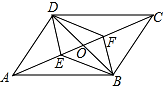• 7．如图，在平行四边形ABCD中，对角线AC，BD相交于点O，E，F是对角线AC上的两点，给出下列四个条件，其中不能判定四边形DEBF是平行四边形的有（　　）

  A．∠ADE=∠CBF

  B．∠ABE=∠CDF

  C．AE=CF

  D．DE=BF
  组卷：248引用：2难度：0.5

  解析

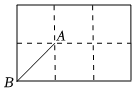• 8．如图，在2×3的方格纸中，小正方形的边长为1，A，B两点在格点上，在图中格点上找一点C，使得△ABC的面积为

  1

  2

  ，满足条件的点C有（　　）

  A．2个

  B．3个

  C．4个

  D．5个
  组卷：334引用：3难度：0.7

  解析

二.解答题（本大题共3个小题，共30分）

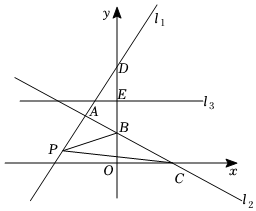• 25．如图，在平面直角坐标系中直线l₁：

  y

  =

  3

  2

  x

  +

  m

  与直线l₂交于点A（-2，3），直线l₂与x轴交于点C（4，0），与y轴交于点B，过BD中点E作直线l₃⊥y轴．
  （1）求直线l₂的解析式和m的值；
  （2）点P在直线l₁上，当S_△PBC=6时，求点P坐标；
  （3）点P是直线l₁上一动点，点Q是直线l₃上一动点，当以P、Q、B、C为顶点的四边形是平行四边形时，求Q点坐标．
  组卷：1967引用：6难度：0.4

  解析

• 26．在▱ABCD中，∠ABC=60°，AB=4，BC=6．点E'在BC边上且BE'=4，将BE'绕点B逆时针旋转a°得到．BE（0°＜a＜180°）．
  （1）如图1，当∠EBA=90°时，求S_△BCE；
  （2）如图2，在旋转过程中，连接CE，取CE中点F，作射线BF交直线AD于点G．
  ①求线段BF的取值范围；
  ②当∠EBF=120°时，求证：BC-DG=2BF；
  （3）如图3．当∠EBA=90°时，点S为线段BE上一动点，过点E作EM⊥射线AS于点M，N为AM中点，直接写出BN的最大值与最小值．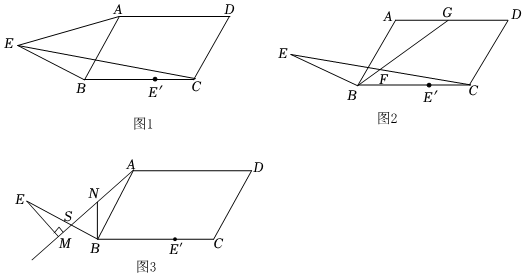
  
  组卷：1416引用：2难度：0.3

  解析