2020-2021学年广东省黄冈中学广州学校九年级(上)月考数学试卷(10月份)
发布:2024/8/18 5:0:1
一、选择题(共十题:共30分)
-
1.用配方法解一元二次方程x2-4x-5=0,此方程可变形为( )
组卷:688引用:22难度:0.9 -
2.关于x的方程kx2-6x+9=0有实数根,k的取值范围是( )
组卷:3360引用:19难度:0.6 -
3.抛物线y=x2+6x+9与x轴交点的个数是( )
组卷:355引用:3难度:0.7 -
4.已知点A(-2,y1)、B(1,y2)在二次函数y=x2+2x+2的图象上,y1与y2的大小关系为( )
组卷:365引用:6难度:0.6 -
5.若x=-1是关于x的一元二次方程ax2-bx-2019=0的一个解,则1+a+b的值是( )
组卷:1192引用:7难度:0.5 -
6.已知x1,x2是关于x的一元二次方程x2-(5m-6)x+m2=0的两个不相等的实根,且满足x1+x2=m2,则m的值是( )
组卷:1520引用:6难度:0.7 -
7.抛物线y=x2+6x+7可由抛物线y=x2如何平移得到的( )
组卷:3332引用:20难度:0.6 -
8.函数y=ax2+c与y=-ax+c(a≠0)在同一坐标系内的图象是图中的( )
组卷:1582引用:4难度:0.6
三、解答题(共八题:共72分)
-
23.如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?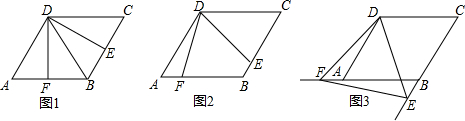 组卷:2161引用:12难度:0.3
组卷:2161引用:12难度:0.3 -
24.如图,抛物线y=ax2+bx-5(a≠0)经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为y=x+n.
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作AM⊥BC于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.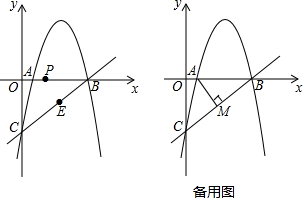 组卷:1820引用:9难度:0.1
组卷:1820引用:9难度:0.1


