2023年贵州省铜仁市某区中考数学四模试卷

一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置作答，每小题3分，共36分.

• 1．-3的相反数是（　　）

  A．3

  B．-3

  C． 1 3

  D． | - 1 3 |
  组卷：226引用：9难度：0.9

  解析

• 2．据有关部门统计，2023年贵州省参加中考的初中毕业生人数预计为550000人，数字550000用科学记数法表示为（　　）

  A．0.55×106

  B．5.5×105

  C．5.5×104

  D．55×104
  组卷：38引用：1难度：0.8

  解析

• 3．围成下列立体图形的各个面中，每个面都是平的是（　　）

  A． 长方体

  B． 圆柱体

  C． 球体

  D． 圆锥体
  组卷：2372引用：16难度：0.8

  解析

• 4．一副直角三角板如图放置，使两三角板的斜边互相平行，每块三角板的直角顶点都在另一三角板的斜边上，则∠1的度数为（　　）

  A．30°

  B．45°

  C．55°

  D．60°
  组卷：964引用：13难度：0.7

  解析

• 5．将直线y=5x向下平移2个单位长度，所得直线的表达式为（　　）

  A．y=5x-2

  B．y=5x+2

  C．y=5（x+2）

  D．y=5（x-2）
  组卷：1677引用：12难度：0.6

  解析

• 6．关于x的方程x²-4x+m=0有两个不相等的实数根，则m的取值范围是（　　）

  A．m＞2

  B．m＜2

  C．m＞4

  D．m＜4
  组卷：1225引用：17难度：0.7

  解析

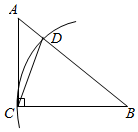• 7．如图，在Rt△ABC中，∠ACB=90°，∠A=50°，以点B为圆心，BC长为半径画弧，交AB于点D，连接CD，则∠ACD的度数是（　　）

  A．50°

  B．40°

  C．30°

  D．20°
  组卷：2270引用：27难度：0.7

  解析

• 8．点A，B在数轴上的位置如图所示，若点A，B表示的数分别为a,b,且满足a+b＞0，则下列选项中原点位置正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：543引用：1难度：0.7

  解析

三、解答题：本大题9小题，共98分，解答应写出必要的文字说明、证明过程或演算步骤。

• 24．已知二次函数y=ax²+bx+c（a≠0）．
  （1）若a=-1，且函数图象经过（0，3），（2，-5）两点，求此二次函数的解析式，直接写出抛物线与x轴交点及顶点坐标；
  （2）在图①中画出（1）中函数的大致图象，并根据图象写出函数值y≥3时自变量x的取值范围；
  （3）若a+b+c=0且a＞b＞c,一元二次方程ax²+bx+c=0两根之差等于a-c,函数图象经过P（

  1

  2

  -c,y₁），Q（1+3c,y₂）两点，试比较y₁、y₂的大小．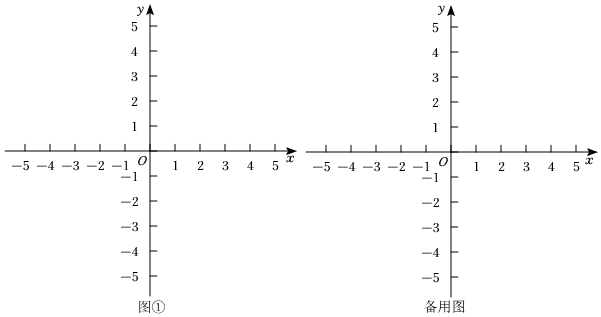
  
  组卷：1018引用：2难度：0.3

  解析

• 25．在△ABC中，AB=AC，∠BAC=α，点P为线段CA延长线上一动点，连接PB，将线段PB绕点P逆时针旋转，旋转角为α，得到线段PD，连接DB，DC．
  （1）如图1，当α=60°时，
  ①求证：PA=DC；
  ②求∠DCP的度数；
  （2）如图2，当α=120°时，请直接写出PA和DC的数量关系．
  （3）当α=120°时，若AB=6，BP=

  31

  ，请直接写出点D到CP的距离为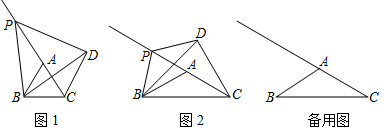

  ．
  
  组卷：4746引用：13难度：0.1

  解析