2023年山东省泰安六中中考数学押题试卷

一、选择题（本大题共12个小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项是符合题目要求.）

• 1．设a是最小的正整数，b是最大的负整数，c是绝对值最小的数，则c-（a-b）的值（　　）

  A．1

  B．-1

  C．0

  D．-2
  组卷：750引用：2难度：0.8

  解析

• 2．下列运算正确的是（　　）

  A．3a2-a2=3	B．a3÷a2=a
  C．（-3ab）2=-6a2b4	D．（a+b）2=a2+ab+b2
  组卷：24引用：2难度：0.8

  解析

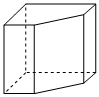• 3．如图所示的几何体的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：66引用：2难度：0.5

  解析

• 4．2022年北京冬奥会国家速滑馆“冰丝带”屋顶上安装的光伏电站，据测算，每年可输出约44.8万度的清洁电力．将44.8万度用科学记数法可以表示为（　　）

  A．0.448×106度	B．44.8×104度
  C．4.48×105度	D．4.48×106度
  组卷：572引用：7难度：0.7

  解析

• 5．如图，等腰直角三角形的顶点A、C分别在直线a、b上，若a∥b,∠1=30°，则∠2的度数为（　　）

  A．30°

  B．15°

  C．10°

  D．20°
  组卷：814引用：11难度：0.9

  解析

• 6．某排球队6名场上队员的身高（单位：cm）是：180，184，188，190，192，194．现用一名身高为186cm的队员换下场上身高为192cm的队员，与换人前相比，场上队员的身高（　　）

  A．平均数变小，方差变小	B．平均数变小，方差变大
  C．平均数变大，方差变小	D．平均数变大，方差变大
  组卷：2702引用：41难度：0.9

  解析

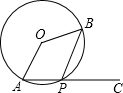• 7．如图，圆心角∠AOB=120°，P是

  ˆ

  AB

  上任一点（不与A，B重合），点C在AP的延长线上，则∠BPC等于（　　）

  A．45°

  B．60°

  C．75°

  D．85°
  组卷：459引用：19难度：0.9

  解析

• 8．若x₁，x₂是方程x²-2mx+m²-m-1=0的两个根，且x₁+x₂=1-x₁x₂，则m的值为（　　）

  A．-1或2

  B．1或-2

  C．-2

  D．1
  组卷：6508引用：38难度：0.9

  解析

三、解答题（本大题共7个小题，共78分，解答应写出文字说明、推理过程或演算步骤。）

• 24．如图①，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A，C重合），在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．
  （1）请直接写出线段AF，AE的数量关系

  ；
  （2）将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；
  （3）在图②的基础上，将△CED绕点C继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．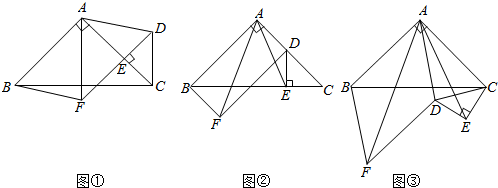
  
  组卷：2666引用：12难度：0.1

  解析

• 25．在平面直角坐标系中，抛物线y=x²-2x-3与x轴相交于点A，B（点A在点B的左侧），与y轴相交于点C，连接AC．
  （1）求点B，点C的坐标；
  （2）如图1，点E（m,0）在线段OB上（点E不与点B重合），点F在y轴负半轴上，OE=OF，连接AF，BF，EF，设△ACF的面积为S₁，△BEF的面积为S₂，S=S₁+S₂，当S取最大值时，求m的值；
  （3）如图2，抛物线的顶点为D，连接CD，BC，点P在第一象限的抛物线上，PD与BC相交于点Q，是否存在点P，使∠PQC=∠ACD，若存在，请求出点P的坐标；若不存在，请说明理由．
  
  组卷：140引用：5难度：0.2

  解析