当前位置：试卷中心 > 试卷详情

2022-2023学年广西钦州四中九年级（下）期中数学试卷

发布：2024/5/23 8:0:8

一、选择题（本大题共12小题，共60分。在每小题列出的选项中，选出符合题目的一项）

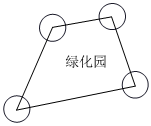1．如图，一块四边形绿化园地，四角都做有半径为2的圆形喷水池，则这四个喷水池占去的绿化园地的面积为（　　）
A．2π B．4π C．6π D．8π
组卷：742引用：6难度：0.6
解析
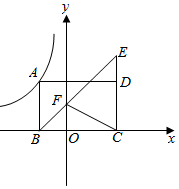2．如图，矩形ABCD中，点A在双曲线y=-
8
x
上，点B，C在x轴上，延长CD至点E，使CD=2DE，连接BE交y轴于点F，连接CF，则△BFC的面积为（　　）
A．5 B．6 C．7 D．8
组卷：5098引用：14难度：0.1
解析
3．下列图形是中心对称图形，也是轴对称图形的是（　　）
A． B． C． D．
组卷：57引用：6难度：0.8
解析
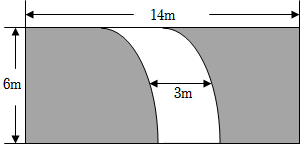4．如图，在一块长14m、宽6m的长方形场地上，有一条弯曲的道路，其余的部分为绿化区，道路的左边线向右平移3m就是它的右边线，则绿化区的面积是（　　）
A．56m² B．66m² C．72m² D．96m²
组卷：2868引用：21难度：0.7
解析
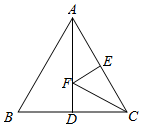5．如图，等边△ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点，若AE=2，当EF+CF取得最小值时，则∠ECF的度数为（　　）
A．15° B．22.5° C．30° D．45°
组卷：3427引用：60难度：0.7
解析
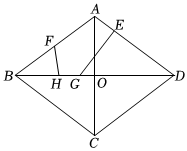6．如图，已知菱形ABCD的对角线AC，BD相交于点O，AC=6，BD=8，点E在AD上，
AE
DE
=
1
3
，点F为AB的中点，点G，H为BD上的动点，GH=1，连接FH，EG，则FH+EG的最小值为（　　）
A．4 B．
17
4
C．
19
4
D．5
组卷：290引用：4难度：0.7
解析
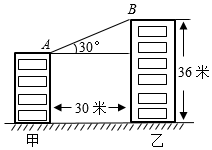7．如图，甲乙两楼相距30米，乙楼高度为36米，自甲楼顶A 处看乙楼楼顶B处仰角为30°，则甲楼高度为（　　）
A．11米 B．（36-15
3
）米 C．15
3
米 D．（36-10
3
）米
组卷：2859引用：15难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共5小题，共40分．解答应写出文字说明，证明过程或演算步骤）

20．如图，AB⊥BC，CD⊥BC，且BC=CD=4cm,AB=1cm,点P以每秒0.5cm的速度从点B开始沿射线BC运动，同时点Q在线段CD上由点C向终点D运动．设运动时间为t秒．
（1）当t=2时，BP=
cm,CP=
cm.
（2）如图①，当点P与点Q经过几秒时，使得△ABP与△PCQ全等？此时，点Q的速度是多少？（写出求解过程）
（3）如图②，是否存在点P，使得△ADP是等腰三角形？若存在，请直接写出t的值，若不存在，请说明理由．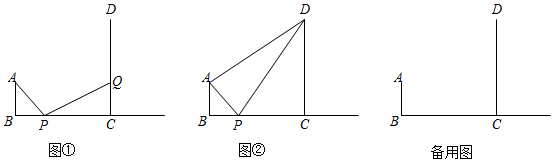
组卷：697引用：10难度：0.2
解析
21．综合与探究
如图1所示，直线y=x+c与x轴交于点A（-4，0），与y轴交于点C，抛物线y=-x²+bx+c经过点A，C．
（1）求抛物线的解析式
（2）点E在抛物线的对称轴上，求CE+OE的最小值；
（3）如图2所示，M是线段OA的上一个动点，过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N．
①若以C，P，N为顶点的三角形与△APM相似，则△CPN的面积为
；
②若点P恰好是线段MN的中点，点F是直线AC上一个动点，在坐标平面内是否存在点D，使以点D，F，P，M为顶点的四边形是菱形？若存在，请直接写出点D的坐标；若不存在，请说明理由．
注：二次函数y=ax²+bx+c（a≠0）的顶点坐标为（-
b
2
a
，
4
ac
-
b
2
4
a
）
组卷：2328引用：5难度：0.1
解析