2014年第二十五届“亚太杯”数学奥林匹克试卷(五年级决赛)
发布:2024/8/6 8:0:9
-
1.计算(27×0.92×0.85)÷(23×1.7×1.8)= .
组卷:178引用:2难度:0.6 -
2.十进制中697改写成七进制为(2014)7,今天是2014年2月23日,计算:(2014)7+(223)7=7.(结果用七进制表示).
组卷:95引用:2难度:0.7 -
3.7个不同的正整数从小到大排列构成等差数列,已知前三个数的平均数是20,后三个数的平均数是24.那么中间三个数的平均数为.
组卷:83引用:2难度:0.6 -
4.如图,正方形ABCD的边长为10,O为其中心,OE⊥OF,则阴影部分面积为
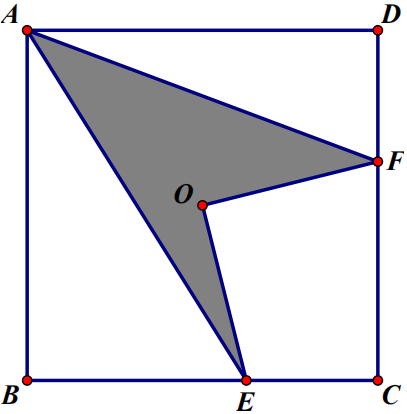 .组卷:18引用:3难度:0.5
.组卷:18引用:3难度:0.5 -
5.小红和小亮玩“石头、剪刀、布”的游戏,约定如果赢了就上三级台阶,输了就下两级台阶,他们从第9级台阶开始玩,玩了12次后(每次都有输赢),小红站在第10级台阶上,则小红共赢了次.
组卷:18引用:2难度:0.6 -
6.根据前面图形数字之间的规律,最后一个图形中?代表的数字是.
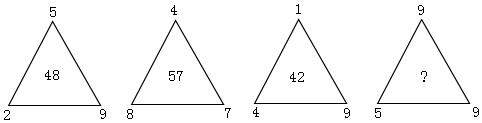 组卷:61引用:1难度:0.6
组卷:61引用:1难度:0.6 -
7.将分数
化成小数,则小数点后第1位到第100位的所有数字的和为.57组卷:17引用:2难度:0.7 -
8.已知a,b是任意自然数,我们规定:a⊕b=a+b+1,a⊗b=a×b-1,那么(5⊕7)×(2⊗4)的值是.
组卷:67引用:1难度:0.5 -
9.小明早上七点整以每分钟52米的速度从家出发去学校,当走到学校时,他手表上的时针与分针刚好分布在数字7的两边且与它的距离相等,已知小明走了不到一小时,那么小明家距离学校米.
组卷:103引用:2难度:0.3 -
10.记号[a]表示不超过a的最大整数,例如
,[0.888…]=0,那么[[175]=3]+[1100]+[2100]+…+[3100]=.865100组卷:109引用:1难度:0.4
-
 29.如图,在△ABC中,AB=13厘米,AC=10厘米,且AH⊥BC.在H与C之间取点D,使∠BAD=60°,∠DAC=2∠HAD.则BH:HC=.组卷:4引用:2难度:0.5
29.如图,在△ABC中,AB=13厘米,AC=10厘米,且AH⊥BC.在H与C之间取点D,使∠BAD=60°,∠DAC=2∠HAD.则BH:HC=.组卷:4引用:2难度:0.5 -
30.将自然数1到7排成一行,满足:每个数或者大于它前面的所有数,或者小于它前面的所有数,(如:4356271满足条件,从第二位开始,3小于首位的4;5大于前两位的4,3;6大于前三位的4,3,5;2小于前四位的4,3,5,6;7大于前五位的4,3,5,6,2;1小于前六位的4,3,5,6,2,7),则满足条件的排列方法中,7不排在第四个位置的排法共有 种.
组卷:3引用:2难度:0.5


