2023年山西省运城市中考数学二模试卷
发布：2024/5/23 8:0:8
一、选择题（本大题共10个小题，每小题3分，共30分.在每个小题给出的四个选项中，只有一项符合题目要求）
-
1．-9的绝对值是（ ）
组卷：530引用：53难度：0.9 -
2．如图所示的是由5个大小相同的小立方块搭成的几何体，则该几何体的左视图为（ ）组卷：25引用：1难度：0.8 -
3．太原市汾河公园北起柴村桥北侧，南至祥云桥南侧，绿化面积为130万平方米，将数据130万用科学记数法可表示为（ ）组卷：52引用：1难度：0.8 -
4．如图，在△ABC中，直线m∥BC，AB⊥m于点D，直线m与AC交于点E，若∠C=20°，则∠A的度数为（ ）组卷：102引用：1难度：0.9 -
5．学校、工厂、企业等单位的大门都是收缩性大门，这种门的门体可以伸缩自由移动，以此来控制门的大小．这种方法应用的数学知识是（ ）组卷：88引用：3难度：0.7 -
6．匀速地向一个如图所示的容器内注水，最后把容器注满．在注水过程中，水面高度h随时间t的变化规律可能是（ ）组卷：218引用：4难度：0.5 -
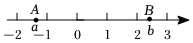7．如图，数轴上的两点A，B对应的实数分别是a,b,则下列不等式成立的是（ ）组卷：85引用：2难度：0.8
三、解答题（本大题共8个小题，共75分，解答应写出必要的文字说明，证明过程或演算步骤）
-
22．综合与实践：
问题情境：在数学活动课上，老师出了这样一道题：
在矩形ABCD中，AB=6，BC=10，将矩形ABCD绕着点C顺时针旋转α到矩形CEFG的位置，点D恰好在边CG上．
问题解决：（1）如图1，连接AC，CF，AF，AF与CG交于点H．
①α的值为 ，AF=；
②求GH的长．
（2）如图2，若将四边形ABCP沿渞直线CP折叠，得到四边形A′PCB′，使得点B的对应点B′恰好在EF上，点A的对应点为A′，点G在A′P上，求AP的长．组卷：283引用：1难度：0.5 -
23．综合与探究：
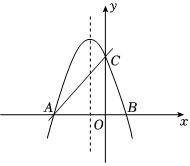
如图，抛物线y=-x2+bx+c与x轴交于点A（-3，0），B（1，0），与y轴交于点C，连接AC．
（1）求抛物线与直线AC的函数表达式；
（2）设Q是抛物线上的一个动点（不与A，B重合），过点Q作QH⊥x轴，垂足为H，交直线AC于点P，当QP=PH时，求点Q的坐标；
（3）在（2）的条件下，抛物线的对称轴上是否存在点D，使得以点C，Q，D为顶点的三角形与△ABC相似，若存在，求点D的坐标；若不存在，请说明理由．组卷：160引用：3难度：0.3
