2022-2023学年山西省太原市部分学校九年级（上）自主测评数学试卷（三）（12月份）
发布：2024/8/11 5:0:1
一、选择题（本大题共10个小题，每小题3分，共30分.在每小题所给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）
-
1．已知△ABC∽△DEF，AB=8cm,DE=12cm,则△ABC与△DEF的相似比是（ ）
组卷：109引用：3难度：0.8 -
2．下列运算正确的是（ ）
组卷：3引用：2难度：0.7 -
3．这几年受疫情的影响，学校经常进行疫情防控讲座，同时选取防控意识强的同学进行演讲，帮助每个学生增强自我保护能力．某校选出五名同学进行演讲比赛，以抽签的方式决定每个人的出场顺序，在盒中放五个看上去完全一样的纸团，纸团里面分别写着表示出场顺序的数字1，2，3，4，5，把纸团充分搅拌后，参加演讲比赛的小军先抽，则小军抽到数字1的概率是（ ）
组卷：33引用：4难度：0.6 -
4．如图1，一棵大树在一次强烈的地震中于离地面5米处折断倒下，树顶落在离树根12米处，图2是这棵大树折断的示意图，则这棵大树在折断之前的高是（ ）
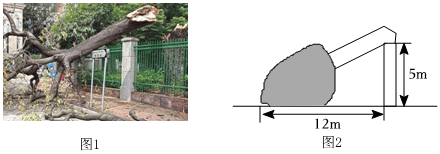组卷：781引用：5难度：0.7 -
5．下面给出的事件中，一定是必然事件的是（ ）
组卷：65引用：8难度：0.7 -
6．把方程x2-12x-3=0化成配方式（x-h）2=k的形式，则下列符合题意的是（ ）
组卷：80引用：5难度：0.6 -
7．如图，在平面直角坐标系中，大鱼与小鱼是关于原点O的位似图形，则下列说法中正确的是（ ）
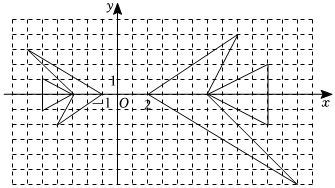组卷：57引用：2难度：0.7
三、解答题（本大题共8个小题，共75分.解答时应写出必要的文字说明、证明过程或演算步骤）
-
22．综合与探究．
问题情境：
如图，在矩形ABCD中，点E为边AD上的动点，点F为边BC上的动点，点M为边AB上的动点，连接EF，过点M作MN⊥EF于点O，交边CD于点N．探究线段FE与MN的比值是否发生变化．
特例探究：
（1）如图2，当点M与点A重合，点F与点B重合，发现．请证明；BEAN=ABAD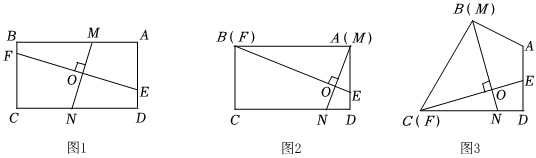
探究发现：
（2）如图1，探究成立吗？若成立，请证明；若不成立，请写出你的发现，并说明理由；EFMN=ABAD
探究拓展：
（3）如图3，把“矩形ABCD”改为“四边形ABCD，BC=CD，∠BCD=60°，∠ADC=90°，点F与点C重合，点M与点B重合”，其余条件不变，猜想的值，并证明．BNCE组卷：361引用：1难度：0.4 -
23．综合与实践
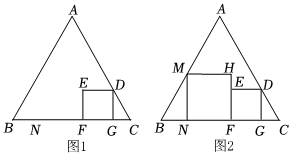
如图，△ABC是等边三角形，BC=6+2，在△ABC内任作一个正方形DEFG，点D在AC上，点E在△ABC内，边FG在BC上．3
（1）尺规作图：在图1中，以点C为位似中心，作正方形DEFG的位似正方形D'E'F'G'，点E'在AB边上，点D'在AC边上，点F'在BC边上（保留作图痕迹，不写作法）；
（2）求（1）中作出的正方形D'E'F'G'的边长；
（3）如图2，当1≤DG≤4时，在△ABC中再放入正方形FHMN，点H在射线FE上，点M在边AB上，边NF在边BC上，直接写出这两个正方形面积和的最大值和最小值．组卷：84引用：2难度：0.2
