2022-2023学年山东省德州五中七年级（下）第一次摸底数学试卷

一、选择题

• 1．下列
  ①

  x

  -

  2

  =

  1

  x

  ；
  ②3x≠11；
  ③

  x

  2

  ＞

  5

  x

  -

  1

  ；
  ④y²-4y=3；
  ⑤x-6；
  ⑥5-4=1，其中是方程的有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：587引用：4难度：0.8

  解析

• 2．下列方程中，解是x=-3的是（　　）

  A．2x+6=1

  B．3x-8=1

  C．3x-1=0

  D．-2x-6=0
  组卷：260引用：8难度：0.8

  解析

• 3．若（m-1）x^|m|=5是关于x的一元一次方程，则m的值是（　　）

  A．±2

  B．±1

  C．1

  D．-1
  组卷：243引用：4难度：0.9

  解析

• 4．下列各式运用等式的性质变形，错误的是（　　）

  A．若m+3=n+3，则m=n	B．若b=c,则 b a = c a
  C．若-m=-n,则m=n	D．若x=y,则1-3x=1-3y
  组卷：165引用：4难度：0.8

  解析

• 5．下列说法是真命题的是（　　）

  A．经过一点只可以画一条直线

  B．过一点有且只有一条直线与已知直线垂直

  C．两点之间线段最短

  D．直线外一点到这条直线的垂线段叫做点到直线的距离
  组卷：197引用：2难度：0.6

  解析

• 6．如图，A、B、C、D是直线上的顺次四点，M、N分别是AB、CD的中点，且MN=6cm,BC=3cm,则AD的长等于（　　）

  A．8cm

  B．9cm

  C．10cm

  D．11cm
  组卷：562引用：3难度：0.7

  解析

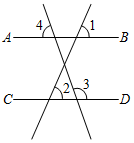• 7．如图，直线AB，CD被两条直线所截，若∠1=64°，∠2=64°，∠3=110°，则∠4的度数为（　　）

  A．110°

  B．70°

  C．64°

  D．46°
  组卷：766引用：8难度：0.7

  解析

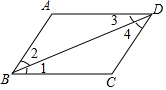• 8．如图，若∠A+∠ABC=180°，则下列结论正确的是（　　）

  A．∠1=∠2

  B．∠2=∠4

  C．∠1=∠3

  D．∠2=∠3
  组卷：991引用：25难度：0.8

  解析

三、解答题

• 24．温州和杭州某厂同时生产某种型号的机器若干台，温州厂可支援外地10台，杭州厂可支援外地4台，现在决定给武汉8台，给南昌6台，每台机器的运费（单位：元）如表：
  

  起点	终点
  	南昌	武汉
  温州厂	400	800
  杭州厂	300	500

  设杭州厂运往南昌的机器为x台．
  （1）用含x的式子表示总运费．
  （2）若总运费为8400元，求杭州厂运往南昌的机器为多少台．
  （3）试问有没有可能使总运费是7900元．若有可能，请写出相应的调动方案；若没有可能，请说明理由．
  组卷：153引用：2难度：0.5

  解析

• 25．问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC度数．
  小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．
  （1）按小明的思路，易求得∠APC的度数为

  度；（直接写出答案）
  （2）问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α，β之间有何数量关系？请说明理由；
  （3）在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α，β之间的数量关系．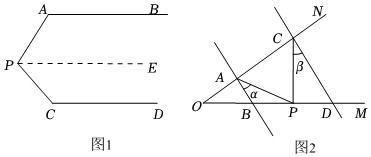
  
  组卷：2253引用：26难度：0.5

  解析