当前位置：试卷中心 > 试卷详情

2023-2024学年辽宁省葫芦岛市长江卫生中等职业技术学校普高班高二（上）第一次月考数学试卷

发布：2024/10/16 1:0:1

1．如图，如空间四边形ABCD中，E，F分别是BC，CD的中点，
AB
+
1
2
BC
+
1
2
BD
=（　　）
A．
AD
B．
AF
C．
FA
D．
EF
组卷：12引用：1难度：0.8
解析
2．O为空间任意一点，若
OP
=
3
4
OA
+
1
8
OB
+
t
OC
，若A，B，C，P四点共面，则t=（　　）
A．1 B．
1
2
C．
1
8
D．
1
4
组卷：4引用：1难度：0.9
解析
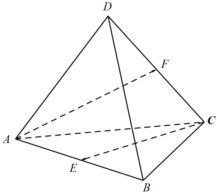3．已知四面体ABCD，所有棱长均为2，点E，F分别为棱AB，CD的中点，则
AF
⋅
CE
=（　　）
A．1 B．2 C．-1 D．-2
组卷：3引用：1难度：0.6
解析
4．已知空间向量
a
，
b
，
|
a
|
=
1
，
|
b
|
=
2
，且
a
-
b
与
a
垂直，则
a
与
b
的夹角为（　　）
A．30° B．45° C．135° D．60°
组卷：28引用：1难度：0.8
解析
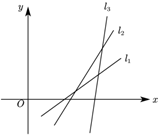5．如图，设直线l₁，l₂，l₃的斜率分别为k₁，k₂，k₃，则k₁，k₂，k₃的大小关系为（　　）
A．k₁＜k₂＜k₃ B．k₁＜k₃＜k₂ C．k₂＜k₁＜k₃ D．k₃＜k₂＜k₁
组卷：64引用：3难度：0.7
解析
6．已知
a
=
（
2
，
0
，
3
）
．
b
=
（
4
，-
2
，
1
）
，
c
=
（
-
2
，
x
,
2
）
，若
（
a
-
b
）
⊥
c
，则x=（　　）
A．4 B．-4 C．2 D．-2
组卷：8引用：1难度：0.8
解析
7．已知空间向量
a
=
（
1
，
2
，
3
）
，
b
=
（
m
,-
1
，
n
）
，若
a
∥
b
，则m+n=（　　）
A．-2 B．-1 C．1 D．2
组卷：9引用：1难度：0.8
解析

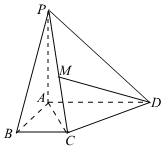21．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M为PC的中点．
（1）求证：PB⊥DM；
（2）求AC与PD所成角的余弦值．
组卷：24引用：1难度：0.7
解析
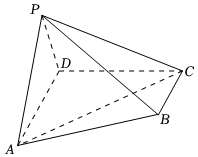22．如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AD∥BC，AD⊥CD，△APD是等腰直角三角形，∠PAD是底角．
（1）求证：平面PAB⊥平面PCD．
（2）若AD=CD=2BC=2，求二面角A-PC-B的余弦值．
组卷：16引用：1难度：0.6
解析

1．如图，如空间四边形ABCD中，E，F分别是BC，CD的中点，AB+12BC+12BD=（ ）