2022-2023学年广西南宁十四中八年级（下）期末数学试卷

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

• 1．水中涟漪（圆形水波）不断扩大，记它的半径为r,则圆周长C与r的关系式为C=2πr.下列判断正确的是（　　）

  A．2是变量

  B．π是变量

  C．r是变量

  D．C是常量
  组卷：506引用：30难度：0.9

  解析

• 2．下列二次根式，最简二次根式是（　　）

  A． 1 5

  B． 0 . 5

  C． 5

  D． 50
  组卷：135引用：5难度：0.7

  解析

• 3．以下列长度的线段为边，能构成直角三角形的是（　　）

  A．1，2，5

  B．1， 3 ，4

  C．2，3，4

  D．3，4，5
  组卷：100引用：5难度：0.7

  解析

• 4．如图是甲，乙两名射击运动员10次射击成绩的折线统计图，根据折线图判断，甲，乙两人成绩更稳定的是（　　）

  A．甲

  B．乙

  C．同样稳定

  D．无法确定
  组卷：49引用：2难度：0.7

  解析

• 5．如图，要测量A，B两点间距离，在O点设桩，取OA中点C，OB中点D，测得CD=3米，则AB的长为（　　）

  A．3米

  B．6米

  C．8米

  D．12米
  组卷：73引用：1难度：0.6

  解析

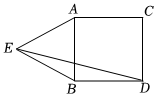• 6．如图，在正方形ABCD外侧作等边△ABE，连接DE，则∠EDB的度数为（　　）

  A．15°

  B．20°

  C．22.5°

  D．30°
  组卷：95引用：1难度：0.5

  解析

• 7．匀速地向一个容器内注水，最后把容器注满，在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为一折线），这个容器的形状是图中的（　　）

  A．

  B．

  C．

  D．
  组卷：6946引用：82难度：0.9

  解析

• 8．一次函数y=-3x+1的图象经过（　　）

  A．第一、二、四象限	B．第一、三、四象限
  C．第一、二、三象限	D．第二、三、四象限
  组卷：279引用：2难度：0.7

  解析

三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤．）

• 25．如图1，将正方形纸片ABCD对折，使得边AB与CD重合，展开铺平，折痕为PQ．然后，再将正方形纸片沿着过点C的直线折叠，此时点B恰好落在折痕PQ的点F处，展开铺平，设CE与PQ交于点G，连接BG，得到图2．
  （1）若正方形ABCD的边长为6，求FQ的长；
  （2）求证：四边形BGFE是菱形；
  （3）如图3，M是正方形ABCD的边AD上一点，连接BM，将△ABM沿着BM折叠，使得点A落在正方形ABCD的内部点K处，连接DK，若正方形ABCD的边长为10，请直接写出DK的最小值．
  
  组卷：189引用：1难度：0.3

  解析

• 26．如图1，抛物线y=ax²+x+c与x轴交于A（-2，0），B（4，0）两点，与y轴交于C．
  （1）求抛物线的解析式；
  （2）点P是直线BC上方抛物线上的—个动点，使△PBC的面积等于△ABC面积的

  1

  4

  ，求点P的坐标；
  （3）过点C作直线l∥x轴，将抛物线在y轴左侧的部分沿直线l翻折，抛物线的其余部分保持不变，得到一个新图象（如图2），请你结合新图象解答：当直线y=-

  1

  2

  x+d与新图象只有一个公共点Q（m,n），且n≥-8时，求d的取值范围．
  
  组卷：271引用：2难度：0.1

  解析