当前位置：试卷中心 > 试卷详情

2023-2024学年湖北省十堰市郧西县九年级（上）期中数学试卷

发布：2024/9/20 5:0:9

一、选择题。（本大题10小题，每小题3分，共30分）

1．如果2是关于x的方程x²-x+n=0的一个根，则n的值为（　　）
A．2 B．-2 C．1 D．-1
组卷：128引用：3难度：0.8
解析
2．下面图形中既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：343引用：13难度：0.9
解析
3．抛物线y=2（x+9）²-3的顶点坐标是（　　）
A．（ 9，3） B．（9，-3） C．（-9，3） D．（-9，-3）
组卷：2998引用：55难度：0.8
解析
4．用配方法解方程x²-6x+8=0时，方程可变形为（　　）
A．（x-3）²=1 B．（x-3）²=-1 C．（x+3）²=1 D．（x+3）²=-1
组卷：303引用：16难度：0.7
解析
5．已知方程x²-5x+2=0的两个根分别为x₁、x₂，则x₁+x₂-x₁x₂的值为（　　）
A．
7
4
B．
9
4
C．7 D．3
组卷：643引用：9难度：0.6
解析
6．如果将抛物线y=x²+2向右平移1个单位，那么所得新抛物线的表达式是（　　）
A．y=x²+3 B．y=（x-1）²+2 C．y=（x+1）²+2 D．y=x²+1
组卷：131引用：10难度：0.7
解析
7．如图，在△ABC中，∠BAC=120°；将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，则下列结论一定正确的是（　　）
A．CB=CD B．DE+DC=BC C．AB∥CD D．∠ABC=∠ADC
组卷：565引用：11难度：0.6
解析
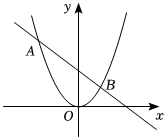8．如图，抛物线y=ax²与直线y=bx+c的两个交点坐标分别为A（-3，9），B（1，1），则关于x的方程ax²-bx-c=0的解为（　　）
A．x₁=-1，x₂=3 B．x₁=9，x₂=-3 C．x₁=1，x₂=9 D．x₁=1，x₂=-3
组卷：1506引用：13难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题。

23．如图1，在△ABC中，∠A=90°，AB=AC=
2
+1，点D，E分别在边AB，AC上，且AD=AE=1，连接DE．现将△ADE绕点A顺时针方向旋转，旋转角为α（0°＜α＜360°），如图2，连接CE，BD，CD．
（1）当0°＜α＜180°时，求证：CE=BD；
（2）如图3，当α=90°时，延长CE交BD于点F，求证：CF垂直平分BD；
（3）在旋转过程中，求△BCD的面积的最大值，并写出此时旋转角α的度数．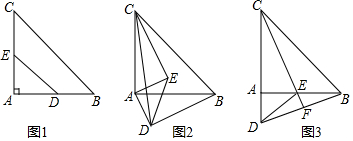
组卷：4272引用：22难度：0.1
解析
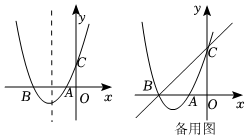24．如图，已知抛物线y=ax²+bx+c与x轴交于A（-1，0）、B（-3，0）两点，与y轴交于C（0，3）．
（1）求抛物线的函数表达式；
（2）设P为对称轴上一动点，求△APC周长的最小值；
（3）若M，N为抛物线上两个动点，分别过点M，N作直线BC的垂线段，垂足分别为D，E．是否存在点M，N使四边形MNED为正方形？如果存在，求正方形MNED的面积；如果不存在，请说明理由．
组卷：456引用：2难度：0.4
解析