当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省常州市天宁区同济中学九年级（上）期中数学试卷

发布：2024/9/13 12:0:8

一、选择题（本大题共8小题，共16分。在每小题列出的选项中，选出符合题目的一项）

1．下列方程中，是关于x的一元二次方程的是（　　）
A．x²+
1
x
2
=0 B．ax²+bx+c=0
C．（x-1）（x+2）=1 D．3x²-2x-5
组卷：352引用：8难度：0.9
解析
2．若一元二次方程x²-2x+m=0有两个不相同的实数根，则实数m的取值范围是（　　）
A．m≥1 B．m≤1 C．m＞1 D．m＜1
组卷：3634引用：47难度：0.9
解析
3．某商品单价经过两次降价从144元降至81元，设平均每次降价的百分率为x,则可列方程（　　）
A．144（1+x）²=81 B．144（1-x）²=81
C．81（1+x）²=144 D．81（1-x）²=144
组卷：392引用：5难度：0.8
解析
4．已知⊙O的半径为5cm,点P在直线l上，且点P到圆心O的距离为5cm,则直线l与⊙O（　　）
A．相离 B．相切 C．相交 D．相交或相切
组卷：214引用：4难度：0.9
解析
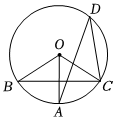5．如图，BC是⊙O的弦，OA⊥BC，∠AOB=76°，则∠ADC的度数是（　　）
A．24° B．35° C．38° D．76°
组卷：415引用：2难度：0.7
解析
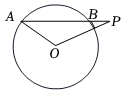6．如图，已知⊙O的半径为5cm,弦AB的长为8cm,P是AB的延长线上一点，BP=2cm,则OP等于（　　）
A．
2
2
cm B．3
2
cm C．
2
5
cm D．
3
5
cm
组卷：1325引用：10难度：0.5
解析
7．如图，点A、B、C、D都在边长为1的网格格点上，以A为圆心，AE为半径画弧，弧EF经过格点D，则扇形AEF的面积是（　　）
A．
5
π
4
B．
9
π
8
C．π D．
π
2
组卷：1718引用：15难度：0.5
解析
8．如图，在平面直角坐标系中，C（0，4），A（3，0），⊙A半径为2，P为⊙A上任意一点，E是PC的中点，则OE的最小值是（　　）
A．1 B．
3
2
C．2 D．
2
组卷：8164引用：14难度：0.2
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：（本大题共7小题，共64分，解答应写出文字说明，证明过程或演算步骤）

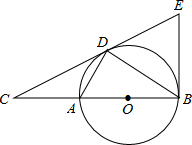24．如图，点D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．
（1）判断直线CD和⊙O的位置关系，并说明理由．
（2）过点B作⊙O的切线BE交直线CD于点E，若AC=2，⊙O的半径是3，求BE的长．
组卷：1326引用：17难度：0.3
解析
25．【概念认识】
自一点引出的两条射线分别经过已知线段的两端，则这两条射线所成的角称为该点对已知线段的视角，如图①，∠APB是点P对线段AB的视角．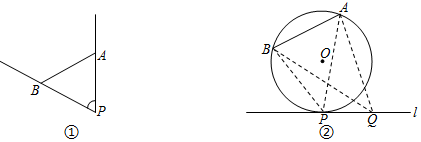

【数学理解】
如图②，已知线段AB与直线l,在直线l上取一点P，使点P对线段AB的视角最大．
（1）过A、B两点，作⊙O使其与直线l相切，切点为P，则点P对线段AB的视角最大，即∠APB最大．
为了证明点P的位置即为所求，不妨在直线l上另外任取一点Q，连接AQ、BQ，证明：∠APB＞∠AQB即可，请完成这个证明．
【问题解决】
在足球电子游戏中，足球对球门的视角越大，越容易被踢进，如果一名球员沿直线带球前进，那么他应当在哪个地方射门，才能使进球的可能性最大？
（2）如图③，A、B是足球门的两端，线段AB是球门的宽，CD是球场边线，∠ADC是直角．
①若该球员沿边线CD带球前进，记足球所在的位置为点P，在图③中，用直尺和圆规在线段CD上求作点P，使点P对AB的视角最大（不写作法，保留作图痕迹）．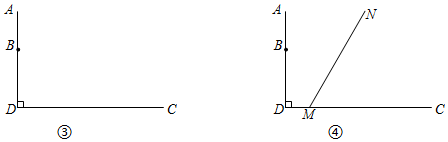

②若M是线段CD上一点，∠CMN=60°，该球员沿射线MN带球前进（如图④），记足球所在的位置为点P，已知AB=4，BD=9，DM=
3
，求点P对AB的最大视角．
组卷：1444引用：4难度：0.3
解析