2022-2023学年新疆兵团第三师图木舒克中学九年级（上）第三次月考数学试卷

一、单选题（共30分）

• 1．下列图形是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：811引用：16难度：0.9

  解析

• 2．一元二次方程3x²-8x-10=0中的一次项系数为（　　）

  A．3

  B．8

  C．-8

  D．-10
  组卷：401引用：7难度：0.9

  解析

• 3．抛物线y=（x+3）²的顶点是（　　）

  A．（0，3）

  B．（0，-3）

  C．（3，0）

  D．（-3，0）
  组卷：221引用：6难度：0.6

  解析

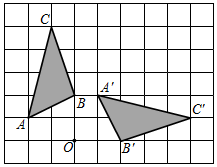• 4．在如图所示的方格纸（1格长为1个单位长度）中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A'B'C'，使各顶点仍在格点上，则其旋转角的度数是（　　）

  A．45°

  B．60°

  C．75°

  D．90°
  组卷：1317引用：20难度：0.8

  解析

• 5．如图，已知长方形的长为10，宽为4，则图中阴影部分的面积为（　　）

  A．20

  B．15

  C．10

  D．25
  组卷：25引用：3难度：0.5

  解析

• 6．已知点A（-1，a），点B（b,2）关于原点对称，则a+b的值是（　　）

  A．-1

  B．1

  C．-2

  D．2
  组卷：174引用：8难度：0.9

  解析

• 7．在下列命题中，正确的是（　　）

  A．长度相等的弧是等弧

  B．直径所对的圆周角是直角

  C．三点确定一个圆

  D．三角形的外心到三角形各边的距离相等
  组卷：259引用：9难度：0.9

  解析

• 8．P为⊙O内一点，OP=3，⊙O半径为5，则经过P点的最短弦长为（　　）

  A．5

  B．6

  C．8

  D．10
  组卷：1348引用：15难度：0.5

  解析

• 9．如图，A，B，C是⊙O上的三个点，若∠C=35°，则∠AOB的度数为（　　）

  A．35°

  B．55°

  C．65°

  D．70°
  组卷：228引用：18难度：0.9

  解析

三、解答题（共60分）

• 28．已知∠ABN=90°，在∠ABN内部作等腰△ABC，AB=AC，∠BAC=α（0°＜α≤90°）．点D为射线BN上任意一点（与点B不重合），连接AD，将线段AD绕点A逆时针旋转α得到线段AE，连接EC并延长交射线BN于点F．
  （1）如图1，当α=90°时，线段BF与CF的数量关系是

  ；
  （2）如图2，当0°＜α＜90°时，（1）中的结论是否还成立？若成立，请给予证明；若不成立，请说明理由；
  （3）若α=60°，AB=4

  3

  ，BD=m,过点E作EP⊥BN，垂足为P，请直接写出PD的长（用含有m的式子表示）．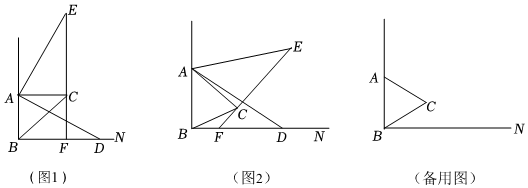
  
  组卷：917引用：3难度：0.5

  解析

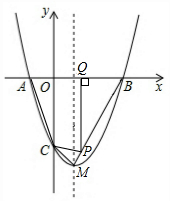• 29．如图，抛物线y=ax²+bx+c与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，且当x=0和x=2时，y的值相等，直线y=3x-7与这条抛物线交于两点，其中一点横坐标为4，另一点是这条抛物线的顶点M．
  （1）求顶点M的坐标并求出这条抛物线对应的函数解析式．
  （2）P为线段BM上一点（P不与点B，M重合），作PQ⊥x轴于点Q，连接PC，设OQ=t,四边形PQAC的面积为S，求S与t的函数解析式，并直接写出t的取值范围．
  （3）在线段BM上是否存在点N，使△NMC为等腰三角形？若存在，直接写出点N的坐标，若不存在，说明理由．
  组卷：389引用：3难度：0.4

  解析