2022-2023学年广东省深圳市罗湖区八年级（上）期末数学试卷

一，选择题（共10小题，每题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．在下列各式中，结果是无理数的是（　　）

  A． 2 + 2

  B． 2 - 2

  C． 2 × 2

  D． 2 2
  组卷：437引用：3难度：0.7

  解析

• 2．下列各组数据中的三个数作为三角形的边长，其中不能构成直角三角形的是（　　）

  A．6，8，10

  B． 2 ， 3 ， 5

  C．5，12，13

  D．3，6，9
  组卷：315引用：1难度：0.6

  解析

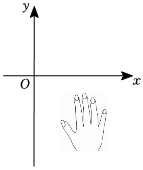• 3．如图，小手盖住的点的坐标可能是（　　）

  A．（2，1）

  B．（-2，3）

  C．（3，-2）

  D．（-2，-1）
  组卷：346引用：3难度：0.7

  解析

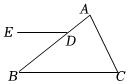• 4．如图，已知△ABC中，若∠A=80°，∠C=60°，D是AB边上一点，DE∥BC，则∠BDE等于（　　）

  A．30°

  B．40°

  C．50°

  D．70°
  组卷：464引用：6难度：0.7

  解析

• 5．下列命题为真命题的是（　　）

  A．两个锐角之和一定是钝角

  B．三角形的外角等于两个内角的和

  C．一个三角形可以有两个钝角

  D．直角三角形的两个锐角和为90°
  组卷：357引用：2难度：0.7

  解析

• 6．把△ABC各点的横坐标都乘以-1，纵坐标不变，符合上述要求的图是（　　）

  A．

  B．

  C．

  D．
  组卷：732引用：3难度：0.9

  解析

• 7．关于函数y=-2x-5，下列说法不正确的是（　　）

  A．图象是一条直线

  B．y的值随着x值的增大而减小

  C．图象不经过第一象限

  D．图象与x轴的交点坐标为（-5，0）
  组卷：739引用：2难度：0.5

  解析

三、解答题（共7小题，共55分，其中第16，17题各6分，第18、19、20题各8分，第21题9分，22题10分）

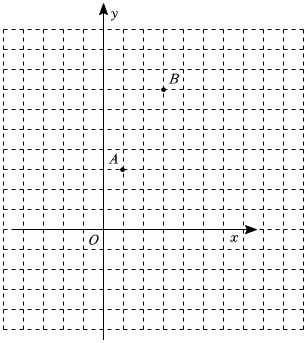• 21．一次函数y=kx+b图象经过点A（1，3）和B（3，7）．
  （1）①画出这个一次函数图象（图中每个小正方形边长都是1个单位）；
  ②试求k与b的值；
  （2）直线AB交x轴于C，交y轴于D，写出C，D两点的坐标：C

  ，D

  ，当x

  时，函数值y＞0．
  （3）过点B作y轴的平行线BM，记点A关于BM的对称点为E，连接CE，AE，P为x轴上一动点，当S_△PCE=2S_△CAE时，求P点坐标．
  ​
  组卷：688引用：1难度：0.5

  解析

• 22．（1）如图1，△ABC是等腰直角三角形，∠C=90°，D为AB中点，E，F分别为AC，BC边上的点，且DE⊥DF，在探究△DEF的形状时，程思同学是这样做的：连接DC，证明△DEC≌△DFB．因此可得DE=DF，同时可得：CE=BF，AE=CF，由此可得出线段AE，BF，EF三者之间满足的等量关系是：

  ；
  （2）如图2，△ABC是非等腰直角三角形，∠C=90°，D为AB中点，E，F分别为AC，BC边上的点，且DE⊥DF，请问（1）中的结论是否仍然成立，请说明理由；
  （3）在（2）的条件下，若AC=8，BC=6，记AE=x,BF=y.
  ①求y关于x的函数关系式；
  ②当DE⊥AB时，AE的长是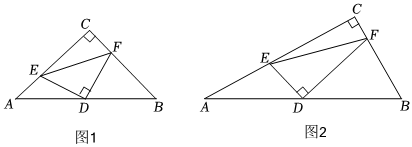

  ．
  
  组卷：1108引用：1难度：0.2

  解析