当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省宿迁市泗阳县九年级（上）期末数学试卷

发布：2024/7/28 8:0:9

一、选择题（本大题共10小题，每小题3分，共30分，每小题只有一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置）

1．方程x²=3x的解为（　　）
A．x=3 B．x=0 C．x₁=0，x₂=-3 D．x₁=0，x₂=3
组卷：2637引用：80难度：0.9
解析
2．一组数据0、-3、2、-2、1的极差是（　　）
A．2 B．3 C．4 D．5
组卷：151引用：3难度：0.7
解析
3．抛物线y=x²-4与y轴的交点坐标是（　　）
A．（0，-4） B．（-4，0） C．（2，0） D．（0，2）
组卷：736引用：10难度：0.9
解析
4．已知
x
y
=
2
5
，则
x
-
y
y
的值为（　　）
A．
2
5
B．
3
5
C．-
2
5
D．-
3
5
组卷：660引用：5难度：0.9
解析
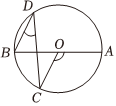5．如图，AB是⊙O直径，∠AOC=140°，则∠D为（　　）
A．40° B．30° C．20° D．70°
组卷：337引用：7难度：0.9
解析
6．对于函数y=（x-2）²+5，下列结论错误的是（　　）
A．图象顶点是（2，5） B．图象开口向上
C．图象关于直线x=2对称 D．函数最大值为5
组卷：743引用：14难度：0.8
解析
7．如图，利用标杆BE测量建筑物的高度，已知标杆BE高2m,测得AB=3m,BC=6m.则建筑物CD的高是（　　）
A．4m B．9m C．8m D．6m
组卷：603引用：2难度：0.5
解析
8．从甲，乙，丙三人中任选两名代表，甲被选中的可能性是（　　）
A．
2
3
B．
1
3
C．
1
4
D．
1
5
组卷：482引用：3难度：0.5
解析
9．若二次函数y=ax²-2ax+c的图象经过点（-1，0），则方程ax²-2ax+c=0的解为（　　）
A．x=-1 B．x₁=3，x₂=1
C．x₁=-1，x₂=-3 D．x₁=3，x₂=-1
组卷：1063引用：4难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共10小题，共96分.解答时应写出必要的步骤、过程或文字说明.）

27．概念生成：定义：我们把经过三角形的一个顶点并与其对边所在直线相切的圆叫做三角形的“切接圆”，如图1，△ABC，⊙O经过点A，并与点A的对边BC相切于点D，则该⊙O就叫做△ABC的切接圆．根据上述定义解决下列问题：
理解应用
（1）已知，Rt△ABC中，∠BAC=90°，AB=6，BC=10．
①如图2，若点D在边BC上，CD=
25
4
，以D为圆心，BD长为半径作圆，则⊙D是△ABC的“切接圆”吗？请说明理由．
②在图3中，若点D在△ABC的边上，以D为圆心，CD长为半径作圆，当⊙D是Rt△ABC的“切接圆”时，求⊙D的半径（直接写出答案）．
思维拓展
（2）如图4，△ABC中，AB=12．AC=BC=10，把△ABC放在平面直角坐标系中，使点C落在y轴上，边AB落在x轴上．试说明：以抛物线y=
1
16
x
2
+4图象上任意一点为圆心都可以作过点C的△ABC的“切接圆”．
组卷：1016引用：4难度：0.2
解析
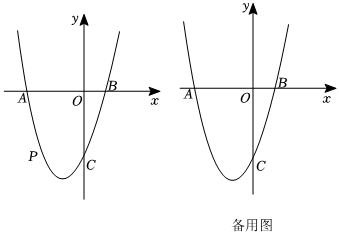28．已知，如图，抛物线y=ax²+bx-8与x轴交于A、B两点，与y轴交于点C，OA=6，OB=
4
3
，点P为x轴下方的抛物线上一点．
（1）求抛物线的函数表达式；
（2）连接AP、CP，求四边形AOCP面积的最大值；
（3）是否存在这样的点P，使得点P到AB和AC两边的距离相等，若存在，请求出点P的坐标；若不存在，请说明理由．
组卷：2508引用：9难度：0.3
解析