2022-2023学年广东省惠州市惠城区惠南学校九年级（上）第一次月考数学试卷

一、选择题（每小题3分，共30分）

• 1．下列方程中，属于一元二次方程的是（　　）

  A．x+y=1

  B．x2+x=1

  C．x+ 1 x =1

  D．x3+x2=1
  组卷：185引用：5难度：0.9

  解析

• 2．将抛物线y=x²向左平移1个单位长度，再向上平移3个单位长度，所得到的抛物线为（　　）

  A．y=（x+1）2+3

  B．y=（x+1）2-3

  C．y=（x-1）2+3

  D．y=（x-1）2-3
  组卷：306引用：4难度：0.7

  解析

• 3．把方程x²-4x-7=0化成（x-m）²=n的形式，下列变形正确的是（　　）

  A．（x-2）2=3

  B．（x-2）2=11

  C．（x-4）2=11

  D．（x+2）2=11
  组卷：190引用：10难度：0.6

  解析

• 4．已知关于x的方程x²+4x+a=0有两个不相等的实数根，则a的值可能为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：544引用：9难度：0.7

  解析

• 5．下列4个图形中，是中心对称图形但不是轴对称的图形是（　　）

  A．

  B．

  C．

  D．
  组卷：129引用：13难度：0.9

  解析

• 6．已知α，β是方程x²+2021x+1=0的两个根，则（1+2022a+α²）（1+2023β+β²）的值为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：116引用：4难度：0.7

  解析

• 7．关于二次函数y=x²-2x-3，下列说法错误的是（　　）

  A．顶点坐标为（1，-4）

  B．对称轴为x=1

  C．抛物线与x轴有两个交点

  D．x=2与x=-2时函数值一样大
  组卷：372引用：5难度：0.8

  解析

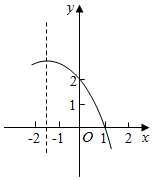• 8．已知二次函数y=ax²+bx+c的部分图象如图所示，则使得函数值y大于2的自变量x的取值可以是（　　）

  A．-4

  B．-2

  C．0

  D．2
  组卷：696引用：28难度：0.6

  解析

五、解答题（三）（每小题10分，共20分）

• 24．商场销售服装，平均每天可售出20件，每件盈利40元，为扩大销售量，减少库存，该商场决定采取适当的降价措施，经调查发现，一件衣服降价1元，每天可多售出2件．
  （1）设每件降价x元，可以销售出

  件．（用x的代数式表示）
  （2）若商场每天要盈利1200元，同时尽量减少库存，每件应降价多少元？
  （3）每件降价多少元时，商场每天盈利达到最大？最大盈利是多少元？
  组卷：570引用：5难度：0.4

  解析

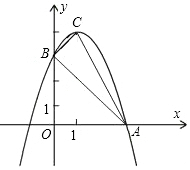• 25．如图，抛物线顶点坐标为点C（1，4），交x轴于点A（3，0），交y轴于点B．
  （1）求抛物线和直线AB的解析式；
  （2）求S_△CAB；
  （3）设点P是抛物线（在第一象限内）上的一个动点，是否存在一点P，使S_△PAB面积最大，若存在，求出P点的坐标；若不存在，请说明理由．
  （4）设点Q是抛物线上的一个动点，是否存在一点Q，使S_△QAB=S_△CAB，若存在，直接写出Q点的坐标；若不存在，请说明理由．
  组卷：1587引用：6难度：0.1

  解析