2023年江苏省连云港市海州区新海实验中学中考数学三模试卷

一、选择题（本大题共有8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上。）

• 1．实数-2023的绝对值是（　　）

  A．2023

  B．-2023

  C． 1 2023

  D．- 1 2023
  组卷：876引用：50难度：0.9

  解析

• 2．下列各式中，计算错误的是（　　）

  A． （ - a ） - 1 = 1 a

  B．a3•a4=a7

  C．（2a2）3=8a6

  D．a3÷a2=a
  组卷：45引用：3难度：0.7

  解析

• 3．已知一组数据：3，-2，4，-3，0，-4，2，这组数据的平均数和极差分别是（　　）

  A．0，8

  B．-1，7

  C．0，7

  D．-1，8
  组卷：125引用：3难度：0.7

  解析

• 4．函数y=

  x

  +

  1

  x

  的自变量的取值范围是（　　）

  A．x≥-1

  B．x≥-1且x≠0

  C．x＞0

  D．x＞-1且x≠0
  组卷：1170引用：12难度：0.7

  解析

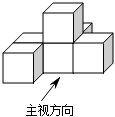• 5．如图，几何体是由六个相同的立方体构成的，则该几何体三视图中面积最大的是（　　）

  A．主视图	B．左视图
  C．俯视图	D．主视图和左视图
  组卷：705引用：11难度：0.8

  解析

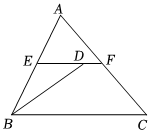• 6．如图，EF是△ABC的中位线，BD平分∠ABC交EF于点D，若AE=3，DF=1，则边BC的长为（　　）

  A．7

  B．8

  C．9

  D．10
  组卷：2965引用：20难度：0.5

  解析

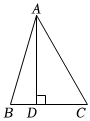• 7．如图，在锐角△ABC中，∠BAC=45°，AD⊥BC于点D．若BD=1，AD=4，则CD的长为（　　）

  A． 3

  B．2

  C． 5

  D．2.4
  组卷：906引用：4难度：0.4

  解析

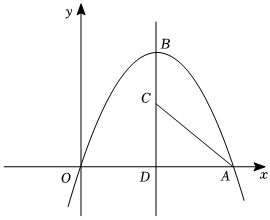• 8．如图，在平面直角坐标系中，抛物线y=

  -

  4

  9

  x

  2

  +

  8

  3

  x

  与x轴的正半轴交于点A，B点为抛物线的顶点，C点为该抛物线对称轴上一点，则3BC+5AC的最小值为（　　）

  A．24

  B．25

  C．30

  D．36
  组卷：2498引用：5难度：0.4

  解析

二、填空题（本大题共有8小题，每小题3分，共24分．不需要写出解答过程，请把答案直接填写在答题卡相应位置上．）

• 9．因式分解：ab²-4a=

  ．
  组卷：3261引用：52难度：0.7

  解析

三、解答题（本大题共11小题，共102分．请在答题卡上指定区域内作答．解答时写出必要的文字说明、证明过程或演算步骤．）

• 26．【阅读材料】
  

  教材习题	如图，AB、CD相交于点O，O是AB中点，AC∥BD，求证：O是CD中点．
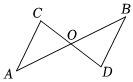
  问题分析	由条件易证△AOC≌△BOD，从而得到OC=OD，即点O是CD的中点
  方法提取	构造“平行8字型”全等三角形模型是证明线段相等的一种常用方法

  请运用上述阅读材料中获取的经验和方法解决下列问题．
  【基础应用】已知△ABC中，∠B=90°，点E在边AB上，点F在边BC的延长线上，连接EF交AC于点D．
  （1）如图1，若AB=BC，AE=CF，求证：点D是EF的中点；
  （2）如图2，若AB=2BC，AE=2CF，探究CD与BE之间的数量关系；
  【灵活应用】如图3，AB是半圆O的直径，点C是半圆上一点，点E是AB上一点，点F在BC延长线上，AB=8，AE=2，

  AE

  CF

  =

  AB

  BC

  ，当点C从点B运动到点A，点D运动的路径长为

  ，CF扫过的面积为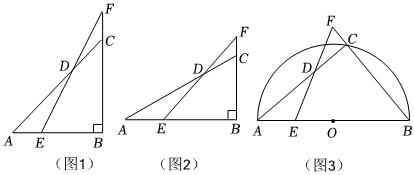

  ．
  
  组卷：474引用：4难度：0.1

  解析

• 27．如图1，平面直角坐标系xOy中，抛物线y=ax²+bx+3（a＜0）与x轴分别交于点A（-3，0）和点B（1，0），与y轴交于点C，P为抛物线上一动点．
  （1）写出抛物线的对称轴为直线

  ，抛物线的解析式为

  ；
  （2）如图2，连结AC，若P在AC上方，作PQ∥y轴交AC于Q，把上述抛物线沿射线PQ的方向向下平移，平移的距离为h（h＞0），在平移过程中，该抛物线与直线AC始终有交点，求h的最大值；
  （3）若P在AC上方，设直线AP，BP与抛物线的对称轴分别相交于点F，E，请探索以A，F，B，G（G是点E关于x轴的对称点）为顶点的四边形面积是否随着P点的运动而发生变化，若不变，求出这个四边形的面积；若变化，说明理由．
  （4）设M为抛物线对称轴上一动点，当P，M运动时，在坐标轴上是否存在点N，使四边形PMCN为矩形？若存在，直接写出点P的横坐标；若不存在，请说明理由．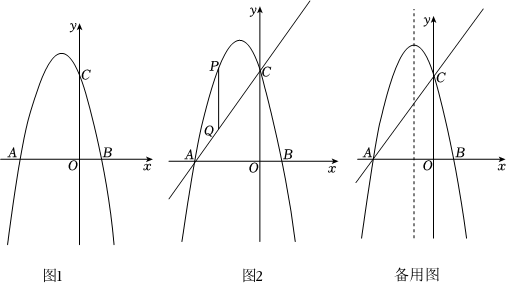
  
  组卷：252引用：5难度：0.3

  解析