2022-2023学年江西省抚州市临川一中九年级（下）期中数学试卷

一、选择题（每小题3分，共18分）每小题只有一个正确选项．

• 1．-3的倒数是（　　）

  A．-3

  B．3

  C． 1 3

  D．- 1 3
  组卷：674引用：194难度：0.9

  解析

• 2．下列运算中正确的是（　　）

  A．b2•b3=b6	B．（2x+y）2=4x2+y2
  C．（-3x2y）3=-27x6y3	D．x+x=x2
  组卷：182引用：8难度：0.8

  解析

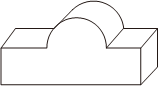• 3．如图所示几何体的左视图是（　　）

  A．

  B．

  C．

  D．
  组卷：75引用：1难度：0.9

  解析

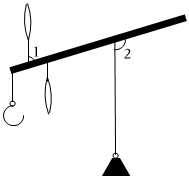• 4．一杆古秤在称物时的状态如图所示，已知∠1=85°，则∠2=（　　）

  A．15°

  B．85°

  C．95°

  D．115°
  组卷：487引用：10难度：0.5

  解析

• 5．下列说法错误的是（　　）

  A．了解市民知晓“礼让行人”交通新规的情况，适合抽样调查

  B．一组数据5，5，3，4，1的众数是5

  C．甲、乙两人跳高成绩的方差分别为S2甲=1.1，S2乙=2.5，则乙的成绩比甲稳定

  D．“经过有交通信号灯的路口，遇到红灯”是随机事件
  组卷：87引用：5难度：0.8

  解析

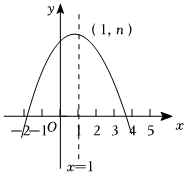• 6．如图所示是抛物线y=ax²+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①a-b+c＞0；②b²-4ac＞0；③3a+c＞0；④一元二次方程ax²+bx+c=n-1没有实数根．其中正确的结论个数是（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：738引用：7难度：0.6

  解析

二、填空题（本大题共6小题，每小题3分，共24分）

• 7．分解因式：4x²-4=

   

  ．
  组卷：666引用：64难度：0.7

  解析

五、（本大题共2个小题，每小题9分，共18分）

• 22．如图1，若抛物线L₁的顶点A在抛物线L₂上，抛物线L₂的顶点B在抛物线L₁上（点A与点B不重合），我们把这样的两抛物线L₁、L₂互称为“伴随抛物线”，可见一条抛物线的“伴随抛物线”可以有多条．
  （1）在图1中，抛物线：L₁：y=-x²+4x-3与L₂：y=a（x-4）²-3互为“伴随抛物线”，则点A的坐标为

  ，a的值为

  ；
  （2）在图2中，已知抛物线L₃：y=2x²-8x+4，它的“伴随抛物线”为L₄，若L₃与y轴交于点C，点C关于L₃的对称轴对称的对称点为D，请求出以点D为顶点的L₄的解析式；
  （3）若抛物线y=a₁（x-m）²+n的任意一条“伴随抛物线”的解析式为y=a₂（x-h）²+k,请写出a₁与a₂的关系式，并说明理由．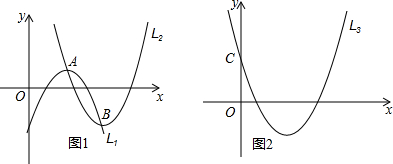
  
  组卷：298引用：4难度：0.3

  解析

六、（本大题共1个小题，共12分）

• 23．定义：如图1，在四边形ABCD中，把对角线BD沿AB翻折后得到BE，把另一条对角线AC绕点A逆时针旋转90°后得到AF，连接EF，CF，则称四边形EBCF为原四边形ABCD的“翻转四边形”．
  特例感知：
  （1）若四边形ABCD为正方形，如图2，延长DA至点E，延长CD至点F，使AE=DF=AD，连接BE，EF．
  ①四边形EBCF是否是正方形ABCD的“翻转四边形“？答：

  （填“是”或“不是”）．
  ②若EF=

  5

  ，则AB=

  ；
  （2）若四边形ABCD为矩形，且AB=2，BC=3，四边形EBCF为矩形ABCD的“翻转四边形”，如图3，求EF的长．
  类比探究：
  （3）在四边形ABCD中，∠BAD=135°，如图4，四边形EBCF为四边形ABCD的“翻转四边形”，且EF²+BC²=BE²，求证：EF∥BC．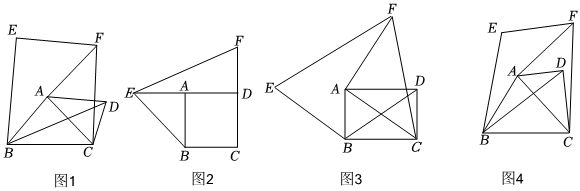
  
  组卷：178引用：1难度：0.1

  解析