2022-2023学年广东省梅州市丰顺一中八年级(上)月考数学试卷(9月份)
发布:2024/8/23 16:0:8
一、选择题(共10题,共30分)
-
1.下列说法中,不正确的是( )
组卷:377引用:13难度:0.9 -
2.下列各式成立的是( )
组卷:266引用:7难度:0.9 -
3.下列式子一定是二次根式的是( )
组卷:3911引用:38难度:0.8 -
4.锐角△ABC中,AB=a-1,AC=a,BC=a+1(a>4),BD⊥AC于点D.则CD-DA的值为( )
组卷:520引用:2难度:0.7 -
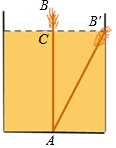 5.如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.则这根芦苇的长度是( )组卷:3477引用:22难度:0.5
5.如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.则这根芦苇的长度是( )组卷:3477引用:22难度:0.5 -
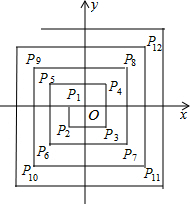 6.如图,在平面直角坐标系中,从点P1(-1,0),P2(-1,-1),P3(1,-1),P4(1,1),P5(-2,1),P6(-2,-2),…依次扩展下去,则P2017的坐标为( )组卷:1084引用:7难度:0.7
6.如图,在平面直角坐标系中,从点P1(-1,0),P2(-1,-1),P3(1,-1),P4(1,1),P5(-2,1),P6(-2,-2),…依次扩展下去,则P2017的坐标为( )组卷:1084引用:7难度:0.7 -
7.已知m=1+
,n=1-2,则代数式2的值为( )m2+n2-3mn组卷:4523引用:71难度:0.9 -
8.已知点A(-4,0),B(6,0),C(3,m),如果△ABC的面积是12,则m的值为( )
组卷:24引用:2难度:0.5
三、解答题(共8题,共62分)
-
24.【阅读】
数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
【理解】
(1)如图1,两个直角边长分别为a、b、斜边长为c的直角三角形和一个两条直角边都是c的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
(2)如图2,n行n列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:n2=;
【运用】
(3)n边形有n个顶点,在它的内部再画m个点,以(m+n)个点为顶点,把n边形剪成若干个三角形,设最多可以剪得y个这样的三角形.当n=3,m=3时,如图3,最多可以剪得7个这样的三角形,所以y=7.
①当n=4,m=2时,如图4,y=;当n=5,m=时,y=9;
②对于一般的情形,在n边形内画m个点,通过归纳猜想,可得y=(用含m、n的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.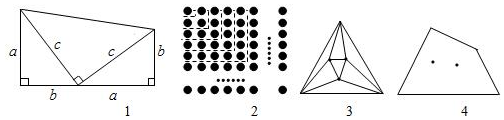 组卷:1556引用:3难度:0.4
组卷:1556引用:3难度:0.4 -
25.阅读材料,回答问题:
(1)中国古代数学著作图1《周髀算经》有着这样的记载:“勾广三,股修四,经隅五.”.这句话的意思是:“如果直角三角形两直角边为3和4时,那么斜边的长为5.”.上述记载表明了:在Rt△ABC中,如果∠C=90°,BC=a,AC=b,AB=c,那么a,b,c三者之间的数量关系是:.
(2)对于这个数量关系,我国汉代数学家赵爽根据“赵爽弦图”(如图2,它是由八个全等直角三角形围成的一个正方形),利用面积法进行了证明.参考赵爽的思路,将下面的证明过程补充完整:
证明:∵S△ABC=,S正方形AEDB=c2,12ab
S正方形MNPQ=.
又∵=,
∴(a+b)2=,4×12ab+c2
整理得a2+2ab+b2=2ab+c2,
∴.
(3)如图3,把矩形ABCD折叠,使点C与点A重合,折痕为EF,如果AB=4,BC=8,求BE的长.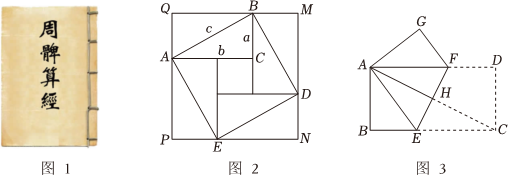 组卷:322引用:6难度:0.1
组卷:322引用:6难度:0.1


