2022-2023学年重庆市渝北区九年级（上）期末数学试卷

一、选择题：（本大题共12小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A，B，C，D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑.

• 1．在实数-2，-4.5，0，2中最小的实数是（　　）

  A．-2

  B．-4.5

  C．0

  D．2
  组卷：69引用：4难度：0.9

  解析

• 2．下列不是轴对称图形是（　　）

  A．

  B．

  C．

  D．
  组卷：67引用：2难度：0.9

  解析

• 3．如图，该图是某池塘一年中pH值的变化，从下列图象中得到的信息正确的是（　　）
  

  A．一年中pH值最高为6.6

  B．2月份的pH值最高

  C．从2月到6月，pH值随着时间的变化而下降

  D．从9月到12月，pH值随着时间的变化而上升
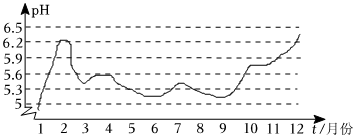  组卷：193引用：3难度：0.6

  解析

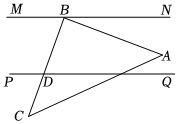• 4．如图，MN∥PQ，将一块三角板ABC如图所示放置，∠ABC=90°，∠BDQ=70°，则∠ABN的度数为（　　）

  A．10°

  B．20°

  C．30°

  D．40°
  组卷：624引用：3难度：0.6

  解析

• 5．已知二次函数y=ax²-4x+c（a≠0）的图象经过点A（1，0）和点B（0，3），则下列说法正确的是（　　）

  A．a＜0	B．对称轴x=4
  C．与y轴的交点为（0，4）	D．顶点坐标（2，-1）
  组卷：187引用：1难度：0.7

  解析

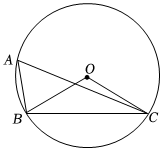• 6．如图，⊙O是△ABC的外接圆，∠BAC=60°，若⊙O的半径为4，则弦BC的长为（　　）

  A．6

  B． 4 2

  C． 4 3

  D． 4 5
  组卷：313引用：1难度：0.7

  解析

• 7．估计

  3

  （

  6

  -

  3

  ）的值应在（　　）

  A．0和1之间

  B．1和2之间

  C．2和3之间

  D．3和4之间
  组卷：219引用：4难度：0.6

  解析

• 8．某公司对外出租一些商铺，第二年每间商铺的租金比第一年多0.1万元，所有商铺第一年的总租金为20万元，第二年总租金为25万元，设每年有x间商铺出租，则可列分式方程为（　　）

  A． 25 x - 20 x = 0 . 1	B． 20 x - 0 . 1 = 25 x
  C． 25 x + 0 . 1 = 20 x	D． 20 x - 25 x = 0 . 1
  组卷：288引用：3难度：0.7

  解析

三、解答题：（本大题9个小题，第17，18小题每小题8分，第19-25小题每小题8分，共86分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上.

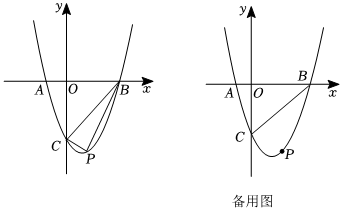• 24．如图，在平面直角坐标系中，抛物线y=ax²+bx-3（a≠0）与x轴交于A（-1，0），B（3，0）两点，与y轴交于C点．
  （1）求抛物线的函数表达式；
  （2）点P是直线BC下方抛物上一动点，连接PB，PC，求△PBC面积的最大值以及此时点P的坐标；
  （3）在（2）中△PBC的面积取得最大值的条件下，将该抛物线沿水平方向向左移动2个单位，平移后的抛物线顶点坐标为Q，M为y轴上一点，在平移后的抛物线上确定一点N，使得以点P，Q，M，N为顶点的四边形是平行四边形，写出所有符合条件的N的坐标，并写出求解点N的坐标的其中一种情况的过程．
  组卷：345引用：1难度：0.2

  解析

• 25．如图，在Rt△ABC中，∠ABC=90°，把边CB绕点C旋转到CF．
  
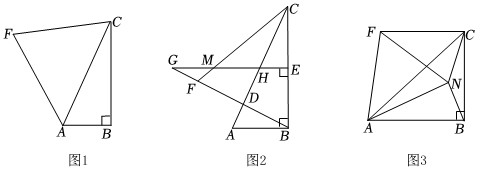
  （1）如图1，连接AF，使FA=FC，BC=2AB=4，求F到AC的距离；
  （2）如图2，连接FB交AC于点D，当BD⊥AC时，在BC边取一个点E，使BE=BA，过点E作BC的垂线交AC于点H，交CF于点M，交BF延长线于点G，求证：BE+GM=MC；
  （3）如图3，若∠BCF=90°，连接AF，点N是Rt△ACB内部一个动点，连接AN、BN使∠NAB=∠CBN，连接CN、NF，若

  AB

  =

  2

  2

  ，

  BC

  =

  6

  ，当CN取最小时，请直接写出△CNF的面积．
  组卷：625引用：4难度：0.1

  解析