2023-2024学年四川省成都外国语学校九年级(上)月考数学试卷(9月份)
发布:2024/8/28 4:0:8
一、选择题(每小题4分,共32分)
-
1.下列是关于x的一元二次方程的是( )
组卷:1969引用:19难度:0.9 -
2.若x1,x2是一元二次方程x2+4x+3=0的两个根,则x1+x2的值是( )
组卷:634引用:10难度:0.9 -
3.若线段a,b,c,d是成比例线段,且a=1cm,b=4cm,c=2cm,则d=( )
组卷:2000引用:22难度:0.9 -
4.菱形ABCD的对角线长分别为6和8,它的面积为( )
组卷:890引用:7难度:0.8 -
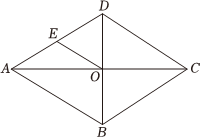 5.如图,菱形ABCD的对角线AC,BD交于点O,点E为边AD的中点,若AC=8cm,BD=6cm,则线段OE的长度是( )组卷:470引用:5难度:0.8
5.如图,菱形ABCD的对角线AC,BD交于点O,点E为边AD的中点,若AC=8cm,BD=6cm,则线段OE的长度是( )组卷:470引用:5难度:0.8 -
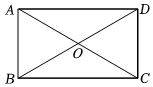 6.如图,矩形ABCD中,对角线AC、BD交于点O.若∠AOB=60°,BD=8,则AB的长为( )组卷:2151引用:34难度:0.8
6.如图,矩形ABCD中,对角线AC、BD交于点O.若∠AOB=60°,BD=8,则AB的长为( )组卷:2151引用:34难度:0.8 -
7.在“双减政策”的推动下,我县某中学学生每天书面作业时长明显减少.2022年上学期每天书面作业平均时长为100min,经过2022年下学期和2023年上学期两次调整后,2023年上学期平均每天书面作业时长为70min.设该校这两学期平均每天作业时长每期的下降率为x,则可列方程为( )
组卷:1366引用:34难度:0.8 -
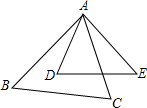 8.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )组卷:6920引用:31难度:0.7
8.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )组卷:6920引用:31难度:0.7
二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
-
25.如图,在矩形ABCD中,点E是BC上的一个动点,过点E作EF⊥BD于点F,EG⊥AC于点G,CH⊥BD于点H,
(1)试证明:CH=EF+EG;
(2)若点E在BC的延长线上,如图2,过点E作EF⊥BD于点F,EG⊥AC的延长线于点G,CH⊥BD于点H,则CH、EF、EG之间有怎样的数量关系,直接写出你的猜想;
(3)如图3,BD是正方形ABCD的对角线,L在BD上,且BL=BC,连接CL,点E是CL上一点,EF⊥BD于点F,EG⊥BC于点G,猜想EF、EG、BD之间具有怎样的数量关系,直接写出你的猜想.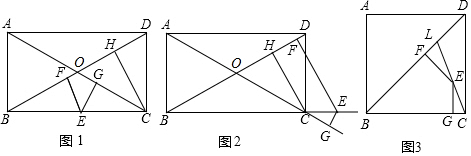 组卷:105引用:2难度:0.2
组卷:105引用:2难度:0.2 -
26.如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,=;AEBD
②当α=180°时,=.AEBD
(2)拓展探究
试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.AEBD
(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.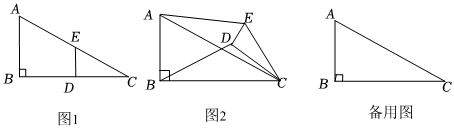 组卷:1299引用:11难度:0.1
组卷:1299引用:11难度:0.1


