2023-2024学年吉林省第二实验学校九年级（上）开学数学试卷

一、选择题（本大题共8小题，每小题3分，共24分）

• 1．4的平方根是（　　）

  A． 2

  B．± 2

  C．2

  D．±2
  组卷：909引用：39难度：0.9

  解析

• 2．下列计算正确的是（　　）

  A．（a3）3=a9

  B．a3•a4=a12

  C．（ab）3=ab3

  D．a6÷a2=a3
  组卷：88引用：5难度：0.8

  解析

• 3．已知x²-8x+a可以写成一个完全平方式，则a可为（　　）

  A．4

  B．8

  C．16

  D．-16
  组卷：4798引用：33难度：0.9

  解析

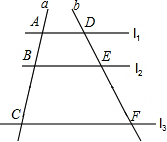• 4．如图，l₁∥l₂∥l₃，直线a,b与l₁、l₂、l₃分别相交于A、B、C和点D、E、F．若

  AB

  BC

  =

  2

  3

  ，DE=4，则EF的长是（　　）

  A． 8 3

  B． 20 3

  C．6

  D．10
  组卷：6098引用：88难度：0.7

  解析

• 5．如图，在△ABC中，∠ACB=90°，AC=3，BC=1，AC在数轴上，点A所表示的数为1，以点A为圆心，AB长为半径画弧，在点A左侧交数轴于点D，则点D表示的数是（　　）

  A． 10

  B． - 10

  C． 1 - 10

  D． 10 - 1
  组卷：195引用：5难度：0.6

  解析

• 6．如图，在直角坐标系中，有两点A（6，3），B（6，0），以原点O位似中心，相似比为

  1

  3

  ，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（　　）

  A．（2，1）

  B．（2，0）

  C．（3，3）

  D．（3，1）
  组卷：4763引用：117难度：0.9

  解析

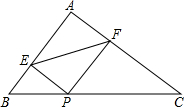• 7．如图，在Rt△ABC中，∠A=90°，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，动点P从点B出发，沿着BC匀速向终点C运动，则线段EP的值大小变化情况是（　　）

  A．一直增大	B．一直减小
  C．先减小后增大	D．先增大后减少
  组卷：61引用：2难度：0.7

  解析

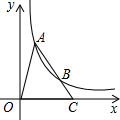• 8．如图，A、B是双曲线上的点，A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C，若S_△AOC=9．则k的值是（　　）

  A．9

  B．6

  C．5

  D．4
  组卷：5141引用：4难度：0.9

  解析

三、解答题（本大题共10小题，共78分）

• 23．【问题探究】在学习三角形中线时，我们遇到过这样的问题：如图①，在△ABC中，点D为BC边上的中点，AB=4，AC=6，求线段AD长的取值范围．我们采用的方法是延长线段AD到点E，使得AD=DE，连结CE，可证△ABD≌△ECD，可得CE=AB=4，根据三角形三边关系可求AD的范围，我们将这样的方法称为“三角形倍长中线”．则AD的范围是：

  ．
  【拓展应用】
  （1）如图②，在△ABC中，BC=2BD，AD=3，AC=2

  10

  ，∠BAD=90°，求AB的长．
  （2）如图③，在△ABC中，D为BC边的中点，分别以AB、AC为直角边向外作直角三角形，且满足∠ABE=∠ACF=30°，连结EF，若AD=2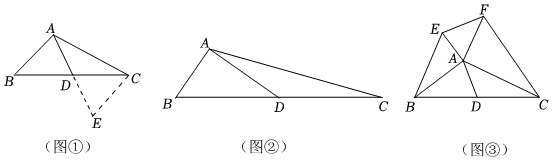

  3

  ，则EF=

  ．（直接写出）
  
  组卷：411引用：5难度：0.4

  解析

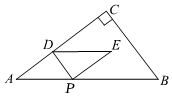• 24．如图，在Rt△ABC中，∠C=90°，AC=8，BC=6．动点P从点A出发，沿AB以每秒5个单位长度的速度向终点B运动，当点P不与点A重合时，过点P作PD⊥AC于点D、PE∥AC，过点D作DE∥AB，DE与PE交于点E．设点P的运动时间为t秒．
  （1）线段AD的长为

  ；（用含t的代数式表示）
  （2）当点E落在BC边上时，求t的值；
  （3）当直线PE将△ABC的面积分成1：3的两部分时，求t的值；
  （4）当点E落在△ABC的角平分线上时，直接写出t的值．
  组卷：190引用：3难度：0.2

  解析