2023-2024学年吉林省松原市乾安县九年级（上）期中数学试卷

一、选择题（本大题共6小题，每小题2分，共12分）

• 1．一元二次方程4x²-6x+1=0的二次项系数、一次项系数、常数项分别是（　　）

  A．4，6，1

  B．4，6，-1

  C．4，-6，1

  D．4，-6，-1
  组卷：264引用：9难度：0.8

  解析

• 2．中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1312引用：59难度：0.8

  解析

• 3．若关于x的一元二次方程x²-3x+m=0有两个相等的实数根，则实数m的值为（　　）

  A．-9

  B． - 9 4

  C． 9 4

  D．9
  组卷：4119引用：58难度：0.5

  解析

• 4．已知二次函数y=-3（x-2）²-3，下列说法正确的是（　　）

  A．对称轴为直线x=-2	B．顶点坐标为（2，3）
  C．函数的最大值是-3	D．函数的最小值是-3
  组卷：3107引用：26难度：0.5

  解析

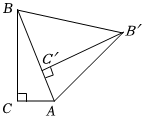• 5．如图，在△ABC中，∠C=90°，∠BAC=70°，将△ABC绕点A顺时针旋转70°，B、C旋转后的对应点分别是B′和C′，连接BB′，则∠BB′C′的度数是（　　）

  A．35°

  B．40°

  C．45°

  D．50°
  组卷：2020引用：33难度：0.7

  解析

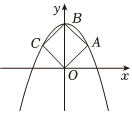• 6．如图，抛物线y=ax²+c经过正方形OABC的三个顶点A，B，C，点B在y轴上，则ac的值为（　　）

  A．-1

  B．-2

  C．-3

  D．-4
  组卷：5324引用：35难度：0.6

  解析

二、填空题（本大题共8小题，每小题3分，共24分）

• 7．已知关于x的方程x²+mx-20=0的一个根是-4，则它的另一个根是

  ．
  组卷：1674引用：17难度：0.6

  解析

• 8．已知一元二次方程x²-3x+1=0有两个实数根x₁，x₂，则x₁+x₂-x₁x₂的值等于

  ．
  组卷：382引用：6难度：0.7

  解析

六、解答题（每小题10分，共20分）26.根据以下素村。探索完成任务。

• 25．我们可以通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整
  原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．
  
  （1）思路梳理
  ∵AB=AD，
  ∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
  ∵∠ADC=∠B=90°，
  ∴∠FDG=180°，点F、D、G共线．
  根据

  ，易证△AFE≌

  ，得EF=BE+DF．
  （2）类比引申
  如图2，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系

  时，仍有EF=BE+DF．
  （3）联想拓展
  如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．
  组卷：5438引用：22难度：0.3

  解析

• 26．根据以下素材，探索完成任务．
  

  如何设计拱桥景观灯的悬挂方案？
  素材1	图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽20m,拱顶离水面5m.据调查，该河段水位在此基础上再涨1.8m达到最高．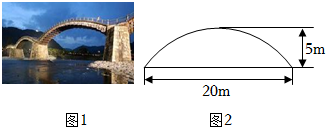
  素材2	为迎佳节，拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼，如图3．为了安全，灯笼底部距离水面不小于1m；为了实效，相邻两盏灯笼悬挂点的水平间距均为1.6m；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．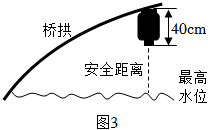
  问题解决
  任务1	确定桥拱形状	在图2中建立合适的直角坐标系，求抛物线的函数表达式．
  任务2	探究悬挂范围	在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围．
  任务3	拟定设计方案	给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标．
  组卷：4133引用：17难度：0.4

  解析