2022-2023学年福建省厦门市集美区杏南中学八年级（上）期中数学试卷

一.选择题：（每题4分，共40分）

• 1．新冠疫情发生以来，各地根据教育部“停课不停教，停课不停学”的相关通知精神，积极开展线上教学．下列在线学习平台的图标中，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：791引用：29难度：0.9

  解析

• 2．五边形的内角和是（　　）

  A．180°

  B．360°

  C．540°

  D．720°
  组卷：1383引用：42难度：0.9

  解析

• 3．下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（　　）

  A．3cm,4cm,10cm	B．8cm,9cm,17cm
  C．13cm,12cm,18cm	D．5cm,5cm,11cm
  组卷：95引用：5难度：0.6

  解析

• 4．a¹⁰可写成（　　）

  A．a5•a5

  B．a5•a2

  C．a5+a5

  D．（a5）5
  组卷：516引用：3难度：0.7

  解析

• 5．在平面直角坐标系中，点（1，2）关于y轴的对称点是（　　）

  A．（1，2）

  B．（-1，2）

  C．（1，-2）

  D．（-1，-2）
  组卷：179引用：5难度：0.9

  解析

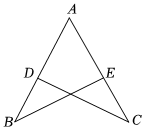• 6．已知：如图，D、E分别在AB、AC上，若AB=AC，AD=AE，∠A=60°，∠B=35°，则∠BDC的度数是（　　）

  A．80°

  B．85°

  C．90°

  D．95°
  组卷：303引用：17难度：0.9

  解析

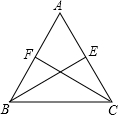• 7．如图，在△ABC中，AB=AC，BE、CF是中线，则由（　　）可得△AFC≌△AEB．

  A．SSS

  B．SAS

  C．AAS

  D．ASA
  组卷：370引用：22难度：0.9

  解析

• 8．若等腰三角形中有一个角等于80°，则这个等腰三角形的顶角的度数为（　　）

  A．100°

  B．80°

  C．80°或20°

  D．50°或80°
  组卷：131引用：8难度：0.8

  解析

三.解答题：（共86分）

• 24．阅读理解：课外兴趣小组活动时，老师提出了如下问题：
  在△ABC中，AB=11，AC=5，BC边上的中线AD的取值范围．
  小明在组内经过合作交流，得到了如下的解决方法（如图1）：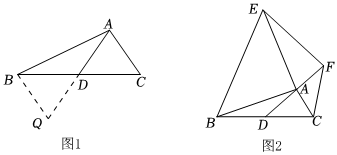
  
  （1）延长AD到Q使得DQ=AD；（2）再连接BQ，把AB、AC、2AD集中在△ABQ中；（3）利用三角形的三边关系可得AQ的取值范围，进而求出AD的取值范围．
  感悟：解题时，条件中若出现“中点”“中线”等条件，可以考虑倍长中线，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中．
  （1）求出AD的取值范围．
  （2）求如图中AC与BQ的位置关系并证明；
  （3）思考：已知，如图2，AD是△ABC的中线，AB=AE，AC=AF，∠BAE=∠FAC=90°，试探究线段AD与EF的关系，并证明．
  组卷：121引用：2难度：0.1

  解析

• 25．在平面直角坐标系中，A（-5，0），B（0，5），点C为x轴正半轴上一动点，过点A作AD⊥BC交y轴于点E．
  
  （1）如图①，若C（3，0），求点E的坐标；
  （2）如图②，若点C在x轴正半轴上运动，且OC＜5，其它条件不变，连接DO，求证：DO平分∠ADC；
  （3）若点C在x轴正半轴上运动，当OC+CD=AD时，求∠OBC的度数．
  组卷：1376引用：21难度：0.1

  解析