2023年江苏省镇江市中考数学二模试卷
发布:2024/6/19 8:0:9
一、填空题(本大题共12小题,每小题2分,共24分。每小题四个备选答案中只有一个符合题目要求。)
-
1.-6的绝对值是 .
组卷:68引用:48难度:0.9 -
2.化简:(2m)2=.
组卷:47引用:1难度:0.7 -
3.分解因式:a2-4a+4=
.组卷:541引用:60难度:0.9 -
4.当x 时,根式
实数范围内有意义.5x+1组卷:46引用:1难度:0.8 -
5.幺米是公认的最小长度单位,1幺米=10-24米,24幺米用科学记数法表示为 米.
组卷:191引用:2难度:0.5 -
6.已知扇形的弧长为6π,半径为12,则这个扇形的圆心角为
度.组卷:77引用:3难度:0.7 -
7.已知二元一次方程组
,则代数式x-y=.3x-y=5x+y=-7组卷:87引用:1难度:0.7 -
8.两个相似三角形的面积比为9:16,则它们的周长之比为
.组卷:146引用:4难度:0.7 -
9.若一组数据1,2,x,4的众数是1,则这组数据的中位数是 .
组卷:189引用:5难度:0.7
三、综合题(本大题共10题,共78分.解答时应写出必要的文字说明、证明过程或演算过程)
-
27.【问题背景】
(1)如图1,在矩形ABCD中,BC=4,点E是BC上一点,连接AE,DE,若∠AEB+∠CED=90°,则AE2+DE2=;
(2)如图2,在正方形ABCD中,AB=6,点E在边CD上,将△ADE沿AE翻折至△AFE,连接CF,求△CEF周长的最小值;
【问题解决】
(3)如图3,某植物园在一个足够大的空地上拟修建一块四边形花圃ABCD,点M是该花圃的一个入口,沿DM和CM分别铺两条小路,且∠DMC=135°,AD+BC=am,AM=30m,BM=40m.管理员计划沿CD边上种植一条绿化带(宽度不计),为使美观,要求绿化带的长度尽可能的长,那么管理员是否可以种植一条满足要求的长度最大的绿化带CD?若可以,求出满足要求的绿化带CD的最大长度(用含a的式子表示);若不可以,请说明理由.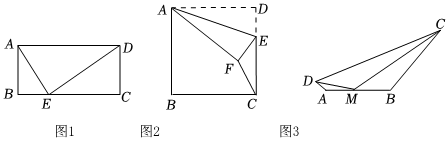 组卷:118引用:1难度:0.1
组卷:118引用:1难度:0.1 -
28.定义:若一个函数的图象上存在横、纵坐标之和为零的点,则称该点为这个函数图象的“平衡点”.例如,点(-1,1)是函数y=x+2的图象的“平衡点”.
(1)在函数①y=-x+3,②y=,③y=-x2+2x+1,④y=x2+x+7的图象上,存在“平衡点”的函数是 ;(填序号)3x
(2)设函数y=-(x>0)与y=2x+b的图象的“平衡点”分别为点A、B,过点A作AC⊥y轴,垂足为C.当△ABC为等腰三角形时,求b的值;4x
(3)若将函数y=x2+2x的图象绕y轴上一点M旋转180°,M在(0,-1)下方,旋转后的图象上恰有1个“平衡点”时,求M的坐标.组卷:1915引用:6难度:0.1


