2023-2024学年江苏省苏州市吴江区汾湖教育集团八年级（上）第一次段考数学试卷
发布：2024/9/20 7:0:8
一、单选题（每小题3分，共8个小题，共24分）
-
1．观察下列图形，是轴对称图形的是（ ）
组卷：25引用：2难度：0.8 -
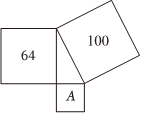2．如图，字母A所代表的正方形的面积为（ ）组卷：309引用：6难度：0.5 -
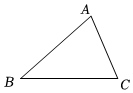3．如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（ ）组卷：967引用：41难度：0.7 -
4．如图，在Rt△ABC中，CD是斜边AB的中线，且BC=8cm,AC=6cm,则CD的长为（ ）
组卷：194引用：4难度：0.5 -
5．如图，△ABC≌△ADE，若∠B=80°，∠DAE=70°，则∠E的度数为（ ）组卷：417引用：10难度：0.5 -
6．学习了勾股定理之后，老师给大家留了一个作业题，小明看了之后，发现三角形各边都不知道，无从下手，心中着急．请你帮助一下小明．如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（ ）组卷：2828引用：10难度：0.5 -
7．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成一个大正方形，设直角三角形较长直角边长为a,较短直角边长为b,若ab=60，大正方形的面积为169．则小正方形的边长为（ ）组卷：352引用：4难度：0.6 -
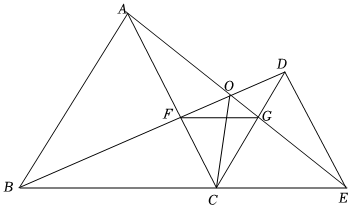8．如图，已知△ABC与△CDE均是等边三角形，点B、C、E在同一条直线上，AE与BD交于点O，AE与CD交于点G，AC与BD交于点F，连接OC、FG，则下列结论：①AE=BD；②AO=OE；③FG∥BE；④CF=CG；⑤∠AOB=60°，其中正确的个数是（ ）组卷：65引用：1难度：0.4
二、填空题（每小题3分，共8个小题，共24分）
-
9．一直角三角形两条直角边长分别为3和4，则该三角形的斜边长为 ．
组卷：1003引用：8难度：0.6
三、解答题（共12个小题，共82分）
-
27．（1）【问题情境】
课外兴趣小组活动时，老师提出了如下问题：
如图①，△ABC中，若AB=13，AC=9，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE=AD，连接BE．请根据小明的方法思考：
Ⅰ．由已知和作图能得到△ADC≌△EDB，依据是．
A．SSS B．SAS C．AAS D．HL
Ⅱ．由“三角形的三边关系”可求得AD的取值范围是．
解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．
（2）【初步运用】
如图②，AD是△ABC的中线，BE交AC于E，交AD于F，且∠FAE=∠AFE．若AE=4，EC=3，求线段BF的长．组卷：306引用：3难度：0.2 -
28．在△ABC中，点D是BC上一点，将△ABD沿AD翻折后得到△AED，边AE交线段BC于点F．
（1）如图1，当∠BAC=90°，DE∥AC时．
①AE和BC有怎样的位置关系，为什么？②若BF=8，EF=4，求线段AB的长．
（2）如图2，若∠C=3∠B，折叠后要使△DEF和△AFC，这两个三角形其中一个是直角三角形而另一个是等腰三角形．求此时∠B的度数．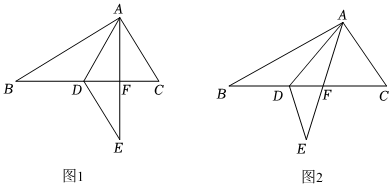
组卷：395引用：4难度：0.2
