2022-2023学年重庆市万州区七年级（下）期末数学试卷

一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡中题号正确答案所对应的方框涂黑。

• 1．下列方程是一元一次方程的是（　　）

  A．x2+2=6

  B．2y+3=0

  C．x+y=9

  D． 2 x + 5 = 8
  组卷：564引用：9难度：0.8

  解析

• 2．利用加减消元法解方程组

  2 x + 5 y = - 10 ①

  5 x - 3 y = 6 ②

  ，下列做法正确的是（　　）

  A．要消去y,可以将①×5+②×2

  B．要消去x,可以将①×3+②×（-5）

  C．要消去y,可以将①×5+②×3

  D．要消去x,可以将①×5+②×（-2）
  组卷：271引用：3难度：0.7

  解析

• 3．中华民族历史悠久，传统文化博大精深．下面选取了几幅传统文化图片，其中，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：122引用：3难度：0.9

  解析

• 4．下列不等式的变形正确的是（　　）

  A．由a＜b,得ac＜bc	B．由a＞b且m≠0，得 - a m ＜ - b m
  C．由ac2＜bc2，得a＜b	D．由a＞b,得ac2＞bc2
  组卷：135引用：1难度：0.6

  解析

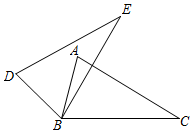• 5．如图，△ABC≌△DBE，∠ABC=80°，∠D=65°，则∠C的度数为（　　）

  A．20°

  B．25°

  C．30°

  D．35°
  组卷：2695引用：17难度：0.7

  解析

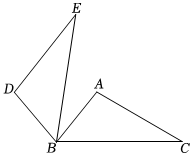• 6．如图，△ABC中，∠ABC=50°，∠C=30°，将△ABC绕点B逆时针旋转α（0°＜α＜90°）得到△DBE，若DE∥AB，则α为（　　）

  A．50°

  B．70°

  C．80°

  D．90°
  组卷：113引用：1难度：0.7

  解析

• 7．中国古代人民很早就在生产生活中发现了许多有趣的数学问题，《孙子算经》中有这样一个问题：今有三人共车，二车空；二人共车，九人步，问人与车各几何．这道题的意思是：今有若干人乘车，每三人共乘一辆车，则剩余两辆车是空的；每两人共乘一辆车，则剩余九个人无车可乘，问车和人各多少．若我们设有x辆车，则可列方程（　　）

  A．3（x-2）=2x+9	B．3（x+2）=2x-9
  C． x 3 +2= x - 9 2	D． x 3 -2= x + 9 2
  组卷：1496引用：16难度：0.6

  解析

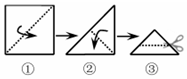• 8．将一张正方形纸片按如图步骤①，②沿虚线对折两次，然后沿③中平行于底边的虚线剪去一个角，展开铺平后的图形是（　　）

  A．

  B．

  C．

  D．
  组卷：1491引用：22难度：0.7

  解析

三、解答题：（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，并画出必要的图形（包括辅助线），请将解答过程书写在答题卷中对应的位置上。

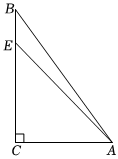• 25．如图，在△ABC中，∠C=90°，a,b,c分别是∠A，∠B，∠C的对边，点E是BC上一个动点（点E与B、C不重合），连AE，若a、b满足|2a-b-10|+（b-6）²=0，且c是不等式组

  x + 12 4 ≤ x + 6

  2 x + 2 3 ＞ x - 3

  的最大整数解．
  （1）求a,b,c的长；
  （2）若AE平分△ABC的周长，求∠BEA的大小；
  （3）是否存在线段AE将三角形ABC的周长和面积同时平分？若存在，求出BE的长；若不存在，请说明理由．
  组卷：57引用：2难度：0.3

  解析

四、解答题：（本大题1个小题，共8分）解答时每小题必须给出必要的演算过程或推理步骤，并画出必要的图形（包括辅助线），请将答案或解答过程书写在答题卷中对应的位置。

• 26．如图，△PBD和△PAC都是直角三角形，∠DBP=∠CAP=90°．
  （1）如图1，PA，PB与直线MN重合，若∠BDP=45°，∠ACP=30°，求∠DPC的度数；
  （2）如图2，若∠BDP=45°，∠ACP=30°，△PBD保持不动，△PAC绕点P逆时针旋转一周．在旋转过程中，
  当AC∥PD时，求∠APN的度数；
  （3）如图3，∠BPA=α（90°＜α＜180°），点E、F分别是线段BD、AC上一动点，当△PEF周长最小时，直
  接写出∠EPF的度数（用含α的代数式表示）．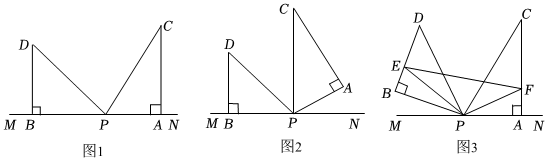
  
  组卷：84引用：1难度：0.3

  解析