2023年山东省青岛市西海岸新区中考数学一模试卷

一、选择题（本大题共10小题，每小题3分，共30分）

• 1．若一个数的绝对值是

  2

  5

  ，则这个数是（　　）

  A． 2 5

  B． - 2 5

  C． 2 5 或 - 2 5

  D． 5 2 或 - 5 2
  组卷：565引用：7难度：0.8

  解析

• 2．剪纸是一项传统的民间文化艺术，也是我国的非物质文化遗产之一，下列剪纸图案中不是中心对称图形的是（　　）

  A．

  B．

  C．

  D．​​​​
  组卷：59引用：2难度：0.9

  解析

• 3．在一个不透明的盒子中装有a个黑白颜色的球，小明又放入了4个红球，这些球大小相同．若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子．通过大量重复试验后，发现摸到红球的频率稳定在20%左右，则a的值大约为（　　）

  A．10

  B．16

  C．25

  D．30
  组卷：191引用：2难度：0.6

  解析

• 4．某中学篮球队12名队员的年龄情况如下表，关于这12名队员的年龄，下列说法中正确的是（　　）
  

  年龄/岁	12	13	14	15	16
  人数	1	3	4	2	2

  A．众数为14

  B．极差为3

  C．中位数为13

  D．平均数为14
  组卷：217引用：3难度：0.6

  解析

• 5．下列运算正确的是（　　）

  A．a2•a3=a6

  B．（-2x）2=4x2

  C． m n - 2 = m 2 n

  D．ab2-ab=b
  组卷：443引用：4难度：0.7

  解析

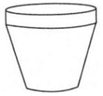• 6．如图所示的是空心花盆的示意图，则它的俯视图是（　　）

  A．

  B．

  C．

  D．
  组卷：114引用：2难度：0.8

  解析

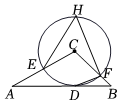• 7．如图，在△ABC中，AC=4，以点C为圆心，2为半径的圆与边AB相切于点D，与AC，BC分别交于点E和点F，点H是优弧EF上一点，∠EHF=70°，则∠BDF的度数是（　　）

  A．35°

  B．40°

  C．55°

  D．60°
  组卷：757引用：5难度：0.6

  解析

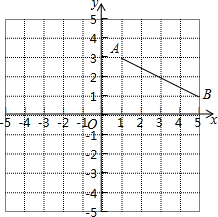• 8．如图，线段AB放在边长为1个单位的小正方形网格中，点A、B均落在格点上，先将线段AB绕点O逆时针旋转90°得到线段A₁B₁，再将线段AB向下平移3个单位得到线段A₂B₂，线段AB，A₁B₁，A₂B₂的中点构成三角形面积为（　　）

  A． 15 2

  B．15

  C．3

  D． 3 2
  组卷：354引用：56难度：0.7

  解析

四、解答题（本大题共9小题，共78分）

• 25．第二十四届冬奥会在北京成功举办，我国选手在跳台滑雪项目中夺得金牌．在该项目中，运动员首先沿着跳台助滑道飞速下滑，然后在起跳点腾空，身体在空中飞行至着陆坡着陆，再滑行到停止区终止．本项目主要考核运动员的飞行距离和动作姿态，某数学兴趣小组对该项目中的数学问题进行了深入研究：
  如图为该兴趣小组绘制的赛道截面图，以停止区CD所在水平线为x轴，过起跳点A与x轴垂直的直线为y轴，O为坐标原点，建立平面直角坐标系．着陆坡AC的坡角为30°，OA=65m,某运动员在A处起跳腾空后，飞行至着陆坡的B处着陆，AB=100m.在空中飞行过程中，运动员到x轴的距离y（m）与水平方向移动的距离x（m）具备二次函数关系，其解析式为y=-

  1

  60

  x²+bx+c.
  （1）求b,c的值；
  （2）进一步研究发现，运动员在飞行过程中，其水平方向移动的距离x（m）与飞行时间t（s）具备一次函数关系，当运动员在起跳点腾空时，t=0，x=0；空中飞行5s后着陆．
  ①求x关于t的函数解析式；
  ②当t为何值时，运动员离着陆坡的竖直距离h最大，最大值是多少？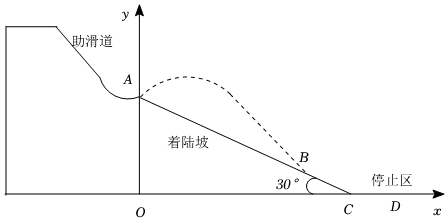
  
  组卷：2949引用：13难度：0.5

  解析

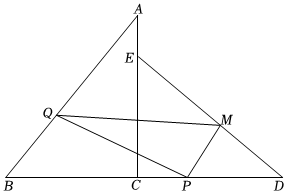• 26．如图，已知Rt△ACB和Rt△DCE中，∠ACB=∠DCE=90°，AC=CD=4，BC=CE=3，B、C、D共线．动点P从D点出发沿DB向B点运动；动点Q从B点出发沿BA向A点运动；速度均为1cm/s,当Q点到达A点时，P，Q两点停止运动，过P点作DE的垂线，垂足为M点，连接PQ，PM，QM（0＜t＜5），解答下列问题：
  （1）当PQ⊥AB时，求t的值；
  （2）设△QPM的面积为S（cm²），求S与t的函数关系式；
  （3）是否存在某一时刻t,使得点Q在PM的垂直平分线上？若存在，求t的值；若不存在，请说明理由．
  组卷：292引用：1难度：0.2

  解析