2023年湖北省随州市广水市中考数学模拟试卷（5月份）

一、选择题（本大题共10小题，每小题3分，共30分，每小题给出的四个选项中，只有一个是正确的）

• 1．下列各数是无理数的是（　　）

  A．2023

  B． 22 7

  C． 8

  D． 3 27
  组卷：70引用：3难度：0.9

  解析

• 2．随着我国经济快速发展，轿车进入百姓家庭，小明同学在街头观察出下列四种汽车标志，其中既是中心对称图形，又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：595引用：26难度：0.9

  解析

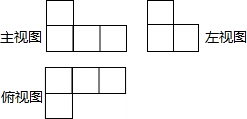• 3．几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：202引用：19难度：0.9

  解析

• 4．在下列计算中，正确的是（　　）

  A．a3+2a3=3a6	B．9a3b÷（-3a）2=ab
  C．a3b•2a2=2a6b	D．（-2a2b）3=-6a3b3
  组卷：67引用：4难度：0.7

  解析

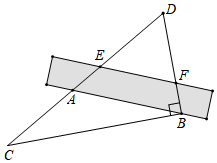• 5．如图，直尺经过一副三角尺中的一块三角板DCB的顶点B，若∠C=30°，∠ABC=20°，则∠DEF度数为（　　）

  A．25°

  B．40°

  C．50°

  D．80°
  组卷：2610引用：21难度：0.7

  解析

• 6．在函数y=

  x

  +

  1

  2

  x

  -

  1

  中，自变量x的取值范围是（　　）

  A．x≥-1

  B．x＞-1且x≠ 1 2

  C．x≥-1且x≠ 1 2

  D．x≤-1且x≠ 1 2
  组卷：476引用：9难度：0.8

  解析

• 7．为了响应学校“书香校园”建设，阳光班的同学们积极捐书，其中宏志学习小组的同学捐书册数分别是：5，7，x,3，4，6．已知他们平均每人捐5本，则这组数据的众数、中位数和方差分别是（　　）

  A．5，5， 3 2

  B．5，5，10

  C．6，5.5， 11 6

  D．5，5， 5 3
  组卷：610引用：8难度：0.7

  解析

• 8．如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S_△DOE：S_△COA=1：25，则S_△BDE与S_△CDE的比是（　　）

  A．1：3

  B．1：4

  C．1：5

  D．1：25
  组卷：2417引用：25难度：0.7

  解析

三、解答题（本题共8小题，共72分，解答应写出必要演算步骤，文字说明或证明过程）

• 23．【探索发现】
  如图①，是一张直角三角形纸片，∠B=90°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为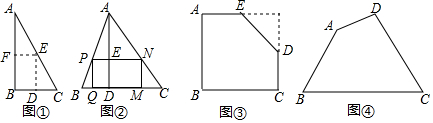

  ．
  
  【拓展应用】
  如图②，在△ABC中，BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为

  ．（用含a,h的代数式表示）
  【灵活应用】
  如图③，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．
  【实际应用】
  如图④，现有一块四边形的木板余料ABCD，经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=

  4

  3

  ，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，求该矩形的面积．
  组卷：2664引用：9难度：0.1

  解析

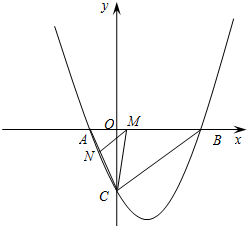• 24．如图，抛物线与x轴交于A（x₁，0）、B（x₂，0）两点，且x₁＜x₂，与y轴交于点C（0，-4），其中x₁，x₂是方程x²-4x-12=0的两个根．
  （1）求抛物线的解析式；
  （2）点M是线段AB上的一个动点，过点M作MN∥BC，交AC于点N，连接CM，当△CMN的面积最大时，求点M的坐标；
  （3）点D（4，k）在（1）中抛物线上，点E为抛物线上一动点，在x轴上是否存在点F，使以A、D、E、F为顶点的四边形是平行四边形？如果存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．
  组卷：1010引用：24难度：0.5

  解析