2022-2023学年江苏省盐城市盐都区鹿鸣路中学八年级（上）期中数学试卷
发布：2024/10/2 3:0:2
一、选择题：（本大题共8小题，每小题2分，共16分）
-
1．下列图案中，不是轴对称图形的是（ ）
组卷：6引用：1难度：0.9 -
2．在平面直角坐标系中，点P（-2，-3）所在的象限是（ ）
组卷：3353引用：48难度：0.7 -
3．下列四组线段中，可以构成直角三角形的是（ ）
组卷：3642引用：128难度：0.9 -
4．下列实数中，无理数的是（ ）
组卷：107引用：3难度：0.7 -
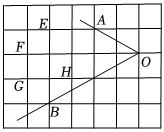5．如图，在正方形网格中，到∠AOB两边距离相等的点可能是（ ）组卷：19引用：2难度：0.7 -
6．下列对△ABC的判断，错误的是（ ）
组卷：954引用：7难度：0.7 -
7．通过如下尺规作图，能确定点D是BC边中点的是（ ）
组卷：1508引用：24难度：0.5 -
8．在平面直角坐标系中，点A的坐标为（-4，3），AB∥y轴，AB=5，则点B的坐标为（ ）
组卷：162引用：6难度：0.5
三、解答题：（本大题共有8小题，其中第19题4分，第20题～24题每题8分，第25题～26题每四10分.共64分.解答需写出必要的文字说明、演算步骤.）
-
25．在平面直角坐标系中，O为坐标原点，过点A（8，6）分别作x轴、y轴的平行线，交y轴于点B，交x轴于点C．
（1）直接写出点B和点C的坐标，其中点B的坐标为 ，点C的坐标为 ；
（2）动点P若从点O出发，沿射线OC以1个单位长度/秒的速度运动，运动时间为t（秒），当△OAP为直角三角形时，求t的值．
（3）动点P若从点B出发，沿B→A→C以2个单位长度/秒的速度向终点C运动，运动时间为t（秒），点D（2，0），连接PD、AD，是否存在这样的t值，使S△APD=S四边形ABOC，若存在，请求出t值，若不存在，请说明理由．112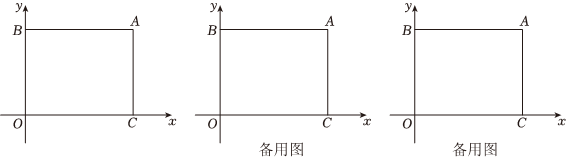
组卷：64引用：2难度：0.3 -
26．【问题提出】如图1，△ABD、△ACE都是等边三角形，求证：BE=DC．
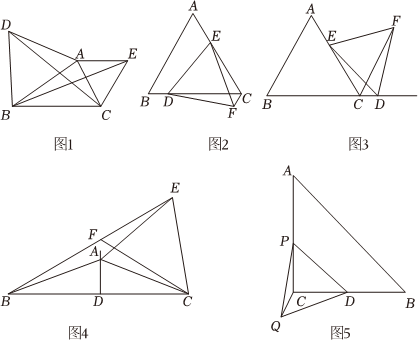
【方法提炼】这两个共顶点的等边三角形，其在相对位置变化的同时，始终存在一对全等三角形，即△ADC≌△ABE．如果把小等边三角形的一边看作“小手”，大等边三角形的一边看作“大手”，这样就类似“大手拉着小手”，不妨称之为“手拉手”基本图形，当图形中只有一个等边三角形时，可尝试在它的一个顶点作另一个等边三角形，构造“手拉手”基本图形，从而解决问题．
【方法应用】
（1）等边三角形ABC中，E是边AC上一定点，D是直线BC上一动点，以DE为一边作等边三角形DEF，连接CF．
①如图2，若点D在边BC上，求证：CE+CF=CD．
②如图3，若点D在边BC的延长线上，线段CE、CF、CD之间的关系为 ．（直接写出结论）
（2）如图4，等腰△ABC中，120°＜∠BAC＜180°，AB=AC，AD⊥BC，且交BC于点D，以AC为边作等边△ACE，直线BE交直线AD于点F，连接FC交AE于点M，写出FE、FA、FC之间的数量关系，并加以说明．
（3）如图5，在△ABC中，∠ACB=90°，AC=BC=8，点D是BC的中点，点P是AC边上的一个动点，连接PD，以PD为边在PD的下方作等边三角形PDQ，连接CQ，则CQ是否有最小值，如有，求出它的最小值；没有，请说明理由．组卷：859引用：4难度：0.5
